Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét (O) có
ΔBDC nội tiếp đường tròn(gt)
BC là đường kính
Do đó: ΔBDC vuông tại D(Định lí)
Xét (O) có
ΔBEC nội tiếp đường tròn(gt)
BC là đường kính
Do đó: ΔBEC vuông tại E(Định lí)
b) Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\widehat{BAD}\) chung
Do đó: ΔADB∼ΔAEC(g-g)
Suy ra: \(\dfrac{AD}{AE}=\dfrac{AB}{AC}\)
hay \(AE\cdot AB=AD\cdot AC\)

B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

bạn đánh câu hỏi vào google
nhập 1 , 2 câu đầu thôi
sẽ hiện ra 1 câu hỏi tương tự như của bạn
NHỚ TICK CHO MÌNH NHA!!!!!!!!!!!!!!!!!!!!

a: Xét (O) có
ΔBEC nội tiếp
BC là đường kính
Do đó: ΔBEC vuông tại E
Xét (O) có
ΔBDC nội tiếp
BC là đường kính
Do đó: ΔBDC vuông tại D
Xét ΔABC có
BD là đường cao
CE là đường cao
BD cắt CE tại H
Do đó: AH⊥BC

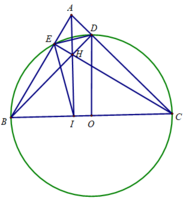
a) Chứng minh AI BC
Ta có ∠BEC = BDC = 90 0 (hai góc nội tiếp chắn nửa đườn tròn)


a) Tứ giác BEHK có hai góc đỉnh E, K là vuông nên bốn đỉnh của tứ giác thuộc đường tròn đường kính EK.
Mặt khác, tứ giác ABKD có bốn đỉnh nằm trên đường tròn đường kính AB. Theo tính chất về các góc nội tiếp cùng chắn một cung thì bằng nhau, ta suy ra \(\angle EKA=\angle EBD=\angle AKD\to AK\) là phân giác của góc EKD.
b) Tứ giác AIKJ có hai góc đỉnh I, J vuông nên các đỉnh của tứ giác nằm trên đường tròn đường kính AK. Do vậy \(\angle IKA=\angle AJI,\angle JKA=\angle AIJ\to\angle IKA=\angle JKA\) (do tính chất tiếp tuyến). Mà AK là phân giác của góc EKD. Suy ra \(\angle IKE=\angle JDA.\)
c) Gọi T là giao điểm AO với IJ. Theo hệ thức liên hệ giữa cạnh góc vuông và hình chiếu trong tam giác vuông, ta có
\(AI^2=AT\cdot AO.\) Do chứng minh trên
\(\angle IKA=\angle AJI=\angle AIJ\to\Delta AIH\sim\Delta AKI\left(g.g\right)\to\frac{AI}{AK}=\frac{AH}{AI}\to AI^2=AH\cdot AK.\)
Vậy ta có \(AT\cdot AO=AH\cdot AK\to\frac{AT}{AH}=\frac{AK}{AO}\to\Delta ATK\sim\Delta AKO\to\angle ATH=\angle AKO=90^{\circ}.\) Do đó ta có \(HT\perp AO\), mà \(IJ\perp AO\) do tính chất tiếp tuyến. Suy ra \(TH\equiv IJ\to I,H,J\) thẳng hàng.