Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
BD là đường cao ứng với cạnh AC
CE là đường cao ứng với cạnh AB
BD cắt CE tại H
Do đó: H là trực tâm của ΔBAC
hay AH\(\perp\)BC tại K
Xét ΔBKH vuông tại K và ΔBDC vuông tại D có
\(\widehat{HBK}\) chung
Do đó: ΔBKH\(\sim\)ΔBDC
Suy ra: \(\dfrac{BK}{BD}=\dfrac{BH}{BC}\)
hay \(BH\cdot BD=BK\cdot BC\)

Kẻ Ax là tiếp tuyến tại A với (O).
Có: xABˆ=ACBˆ(=12sđAB⌢)
Xét ΔvABDΔvABD, có:
BACˆBAC^: chung;
⇒ΔvABD∼ΔvACE(gn)⇒ΔvABD∼ΔvACE(gn)
⇒ABAD=AEAC⇒ABAD=AEAC
mà BACˆBAC^ chung
⇒ΔADE∼ΔABC(cgc)⇒ΔADE∼ΔABC(cgc)
⇒AEDˆ=ACBˆ=xABˆ⇒AED^=ACB^=xAB^(ở vị trí SLT)
⇒Ax//DE
mà Ax⊥OA NÊN DE⊥OA
Ta có: AM là đường cao thứ 3( đi qua trực tâm H)
Xét ΔBMHΔBMH và ΔBDCΔBDC có:
BMHˆ=BDCˆ(=900)BMH^=BDC^(=900)
BˆB^ chung
⇒ΔBMH≈ΔBDC(g−g)⇒ΔBMH≈ΔBDC(g−g)
⇒BMBD=BHBC⇒BMBD=BHBC⇔BD.BH=BM.BC(1)⇔BD.BH=BM.BC(1)
Xét ΔCMHΔCMH và ΔCEBΔCEB có:
CMHˆ=CEBˆ(=900)CMH^=CEB^(=900)
CˆC^ chung
⇒ΔCMH=ΔCEB(g−g)⇒ΔCMH=ΔCEB(g−g)
⇒CMCH=CECB⇔CH.CE=BC.CM(2)⇒CMCH=CECB⇔CH.CE=BC.CM(2)
Cộng (1) và (2) vế theo vế, ta được:
BD.BH+CH.CE=BM.BC+BC.CMBD.BH+CH.CE=BM.BC+BC.CM
⇒BD.BH+CH.CE=BC.(BM+CM)=BC2(đpcm)⇒BD.BH+CH.CE=BC.(BM+CM)
=BC2(đpcm)

Do ^AEH=^ADH=90o nên tứ giác AEHD nội tiếp đường tròn.
Suy ra đường tròn ngoại tiếp tam giác AED chính là đường tròn đường kính AH.
Do H là giao điểm hai đường cao BD và CE nên H là trực tâm. Thế thì AH ⊥ BC.
Suy ra ^DAH=^DBC (vì cùng phụ với góc ^DCB).
Tam giác BDC vuông tại D có I là trung điểm của BC nên IB = ID = IC.
Suy ra tam giác IBD cân ở I. Vì vậy ^IDB=^DBI.
Từ đó suy ra: ^HAD=^HBI=^BDI hay ^HAD=^HDI.
Gọi J là trung điểm AH. Ta có ^HAD=^JDA⇒^JDA=^HDI.
Vậy nên ^JDI=^HDI+^JDH=^JDA+^FDH=^ADH=90o.
Suy ra DI là tiếp tuyến của đường tròn đường kính AH.
Chứng minh tương tự ta cũng có EI là tiếp tuyến của đường kính AH.
Do \widehat{AEH}=\widehat{ADH}=90^oAEH=ADH=90o nên tứ giác AEHD nội tiếp đường tròn.
Suy ra đường tròn ngoại tiếp tam giác AED chính là đường tròn đường kính AH.
Do H là giao điểm hai đường cao BD và CE nên H là trực tâm. Thế thì AH \perp⊥ BC.
Suy ra \widehat{DAH}=\widehat{DBC}DAH=DBC (vì cùng phụ với góc \widehat{DCB}DCB).
Tam giác BDC vuông tại D có I là trung điểm của BC nên IB = ID = IC.
Suy ra tam giác IBD cân ở I. Vì vậy \widehat{IDB}=\widehat{DBI}IDB=DBI.
Từ đó suy ra: \widehat{HAD}=\widehat{HBI}=\widehat{BDI}HAD=HBI=BDI hay \widehat{HAD}=\widehat{HDI}HAD=HDI.
Gọi J là trung điểm AH. Ta có \widehat{HAD}=\widehat{JDA}\Rightarrow\widehat{JDA}=\widehat{HDI}HAD=JDA⇒JD<...

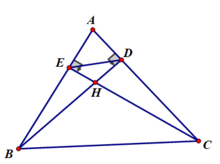
b) Xét tứ giác BDEC có:
∠(BEC) = ∠(BDC) = 90 0
Mà 2 góc này cùng nhìn cạnh BC
⇒ Tứ giác BDEC là tứ giác nội tiếp

3:
Xét ΔGMB và ΔGCA có
góc GMB=góc GCA
góc G chung
=>ΔGMB đồng dạng với ΔGCA
=>GM/GC=GB/GA
=>GM*GA=GB*GC
Xét ΔGEB và ΔGCD có
góc GEB=góc GCD
góc EGB chung
=>ΔGEB đồng dạng với ΔGCD
=>GE/GC=GB/GD
=>GE*GD=GB*GC=GM*GA
=>GE/GA=GM/GD
=>ΔGEM đồng dạng với ΔGAD
=>góc GEM=góc GAD
=>góc DEM+góc DAM=180 độ
=>ADEM nội tiếp
=>góc MDE=góc MAE
A B C D E H M
Kẻ HM vuông góc BC ( M thuộc BC )
\(\Delta BHM~\Delta BCD\left(g.g\right)\) \(\Rightarrow\frac{BH}{BC}=\frac{BM}{BD}\Rightarrow BH.BD=BC.BM\) ( 1 )
\(\Delta CHM~\Delta CBE\left(g.g\right)\Rightarrow\frac{CH}{BC}=\frac{CM}{CE}\Rightarrow CH.CE=BC.CM\) ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow BH.BD+CH.CE=BC\left(BM+CM\right)=BC^2\)