Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔAHB vuông tại H có HM là đường cao ứng với cạnh huyền AB
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao ứng với cạnh huyền AC
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)

Áp dụng hệ thức lượng trong tam giác vuông ABH với đường cao BM:
\(AH^2=AM.AB\) (1)
Áp dụng hệ thức lượng trong tam giác vuông ACH với đường cao CN:
\(AH^2=AN.AC\) (2)
(1);(2)\(\Rightarrow AM.AB=AN.AC\)

+Xét tứ giác ANHM:
AMH^ = 90o (HM _|_ AB)
ANH^ = 90o (HN _|_ AC)
=> AMH^ + ANH^ = 180o => tứ giác ANHM nội tiếp
+ Ta có: AMN^ = AHN^ (cùng chắn cung AN của (ANHM))
AHN^ = ACB^ (cùng phụ HNC^)
=> AMN^ = ACB^
+Xét tam giác AMN và tam giác ACB:
A^ chung (gt);
AMN^ = ACB^ (cmt)
=> tam giác AMN đồng dạng tam giác ACB (g.g)
\(\Rightarrow\dfrac{AM}{AN}=\dfrac{AC}{AB}\Rightarrow AB\cdot AM=AN\cdot AC\left(đpcm\right)\)

a: Xét ΔABC vuông tại A có sin C=AB/BC=3/5
=>cos C=căn 1-(3/5)^2=4/5
=>AC/BC=4/5
=>BC=20(cm)
\(AB=\sqrt{20^2-16^2}=12\left(cm\right)\)
ΔABC vuông tại A có AH là đường cao
nên CH*CB=CA^2
=>CH*20=16^2=256
=>CH=12,8(cm)
b: ΔHAB vuông tại H có HM là đường cao
nên AM*AB=AH^2
ΔHAC vuông tại H có HN là đường cao
nên AN*AC=AH^2
=>AM*AB=AN*AC
=>AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN đồng dạng với ΔACB

a: góc NED+góc NCD=180 độ
=>NEDC nội tiếp
b: ΔAHB vuôg tại H có HM vuông góc AB
nên AM*AB=AH^2
ΔAHC vuông tại H có HN vuông góc AC
nên AN*AC=AH^2
=>AM*AB=AN*AC

Lời giải:
a. Áp dụng hệ thức lượng trong tam giác vuông:
$AM.AB=AH^2$
$AN.AC=AH^2$
$\Rightarrow AM.AB=AN.AC$ (đpcm)
b.
Vì $AM.AB=AN.AC\Rightarrow \frac{AM}{AN}=\frac{AC}{AB}$
Xét tam giác $AMN$ và $ACB$ có:
$\widehat{A}$ chung
$\frac{AM}{AN}=\frac{AC}{AB}$ (cmt)
$\Rightarrow \triangle AMN\sim \triangle ACB$ (c.g.c)
Ta có đpcm.
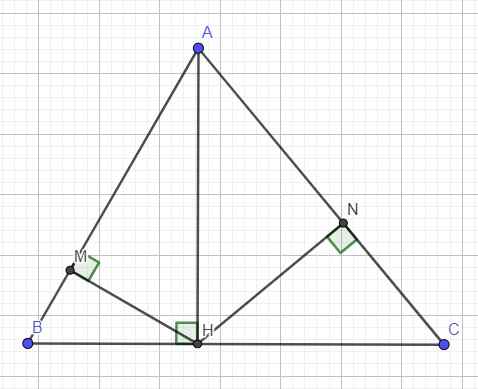
Xét tứ giác AMHN có góc ANM = góc AHM (1) (2 góc trong tứ giác nội tiếp cùng nhìn xuống cạnh AM)
Mà góc AHM = góc B = 90o – BHM (2)
(1)(2) => góc ANM = góc B
Xét tam giác ANM và tam giác ABC có:
Góc A chung
Góc ANM = góc B
ð tam giác ANM đồng dạng tam giác ABC (g – g)
ð AN/AB = AM/AC
ð AN.AC = AB.AM