Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hình bạn tự vẽ nha.
a) Xét tam giác ADB và tam giác AEC có:
góc BAC là góc chung
góc ADB =góc AEC
Suy ra: Tam giác ADB đồng dạng với tam giác AEC (g.g)
=> AD/AE = AB/AC (cạnh tương ứng)
=> AD/AB = AE/AC
Xét tam giác AED và tam giác ACB có:
góc BAC là góc chung
AD/AB = AE/AC (cmt)
Suy ra tam giác AED đồng dạng với tam giác ACB (c.g.c)
b) Gọi giao điểm của AH và BC là K.
Xét tam giác ABC có
BD và CE là 2 đường cao mà chúng cắt nhau tại H
nên H là trực tâm của tam giác ABC
=>AK vuông góc với BC
Xét tam giác BKH và tam giác BDC có:
góc HBK là góc chung
góc BKH = góc BDC
Suy ra BD/BK = BC/BH
=> BD.BH = BC.BK (1)
Chứng minh tương tự ta cũng có : tam giác CKH đồng dạng với tam giác CEB
=> CK/CE = CH/CB
=> CE.CH = BC.CK (2)
Lấy (1)+(2) ta được đpcm

Kẻ \(HM\perp BC\)
Xét \(\Delta BHM\) và \(\Delta BCD\) ta có:
\(\widehat{BMH}=\widehat{BDC}=90^o\)
\(\widehat{CBD}\) chung
\(\Rightarrow\Delta BHM\sim\Delta BCD\left(g.g\right)\)
\(\Rightarrow\dfrac{BM}{BD}=\dfrac{BH}{BC}\Rightarrow BM\times BC=BH\times BD\left(1\right)\)
Xét \(\Delta CMH\) và \(\Delta CEB\) ta có:
\(\widehat{BCE}\) chung
\(\widehat{CMH}=\widehat{CEB}=90^o\)
\(\Rightarrow\Delta CMH\sim\Delta CEB\left(g.g\right)\)
\(\Rightarrow\dfrac{CH}{CB}=\dfrac{CM}{CE}\Rightarrow CM\times CB=CH\times CE\left(2\right)\)
Cộng 2 vế của (1)(2) lại với nhau ta đc:
\(BM.BC+CM.CB=BH.BD+CH.CE\)
\(\Leftrightarrow BC\left(BM+CM\right)=BH.BD+CH.CE\)
\(\Rightarrow BC^2=BH.BD+CH.CE\left(đcpcm\right)\)
Vậy..............

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
AB=AC
\(\hat{DAB}\) chung
Do đó: ΔADB=ΔAEC
b: ΔADB=ΔAEC
=>DB=EC và AD=AE
Ta có: AE+EB=AB
AD+DC=AC
mà AE=AD và AB=AC
nên EB=DC
Xét ΔEBC vuông tại E và ΔDCB vuông tại D có
BC chung
EB=DC
Do đó: ΔEBC=ΔDCB
=>\(\hat{ECB}=\hat{DBC}\)
=>\(\hat{HBC}=\hat{HCB}\)
=>ΔHBC cân tại H
c: ta có: HB=HC
HC>HD(ΔHDC vuông tại D)
DO đó: HB>HD
d: Xét ΔHNB và ΔHMC có
HN=HM
\(\hat{NHB}=\hat{MHC}\) (hai góc đối đỉnh)
HB=HC
Do đó: ΔHNB=ΔHMC
=>NB=MC
Gọi K là giao điểm của BN và CM
Ta có: BM=BH+HM
CN=CH+HN
mà BH=CH và HM=HN
nên BM=CN
Xét ΔBNM và ΔCMN có
BN=CM
BM=CN
MN chung
Do đó: ΔBNM=ΔCMN
=>\(\hat{BNM}=\hat{CMN}\)
=>\(\hat{KMN}=\hat{KNM}\)
=>KM=KN
ta có; KB+BN=KN
KC+CM=KM
mà BN=CM và KN=KM
nên KB=KC
=>K nằm trên đường trung trực của BC(1)
ta có: HB=HC
=>H nằm trên đường trung trực của BC(2)
ta có: AB=AC
=>A nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,H,K thẳng hàng
=>AH,BN,CM đồng quy tại K

a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
\(\hat{DAB}\) chung
Do đó: ΔADB~ΔAEC
b: Xét ΔFEB vuông tại E và ΔFDC vuông tại D có
\(\hat{EFB}=\hat{DFC}\) (hai góc đối đỉnh)
Do đó: ΔFEB~ΔFDC
=>\(\frac{EF}{DF}=\frac{EB}{DC}\)
=>\(EF\cdot DC=EB\cdot DF\)
c: Ta có: BH⊥BA
CF⊥AB
Do đó: BH//CF
Ta có: BF⊥CA
CH⊥CA
Do đó: BF//CH
Xét tứ giác BFCH có
BF//CH
BH//CF
Do đó: BFCH là hình bình hành
=>BC cắt FH tại trung điểm của mỗi đường
mà G là trung điểm của BC
nên G là trung điểm của FH
Xét ΔAFH có
G,I lần lượt là trung điểm của FH,FA
=>GI là đường trung bình của ΔAFH
=>GI//AH và \(GI=\frac12AH\)
=>AH=2GI
ΔEBC vuông tại E
mà EG là đường trung tuyến
nên GE=GB=GC
Xét ΔGEB có \(\hat{EGC}\) là góc ngoài tại đỉnh G
nên \(\hat{EGC}=\hat{GEB}+\hat{GBE}=2\cdot\hat{GBE}=2\cdot\hat{ABC}\) (1)
ΔAFE vuông tại E
mà EI là đường trung tuyến
nên IE=IF=IA
Xét ΔEIF có \(\hat{EIA}\) là góc ngoài tại đỉnh I
nên \(\hat{EIA}=\hat{IEF}+\hat{IFE}=2\cdot\hat{IFE}\) (2)
Xét ΔABC có
BD,CE là các đường cao
BD cắt CE tại F
Do đó: F là trực tâm của ΔABC
=>AF⊥BC
=>\(\hat{FAB}+\hat{ABC}=90^0\)
mà \(\hat{FAB}+\hat{AFE}=90^0\)
nên \(\hat{ABC}=\hat{AFE}\) (3)
Từ (1),(2),(3) suy ra \(\hat{EIA}=\hat{EGC}\)

Gợi ý: Gọi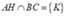 , chứng minh được AK ^ BC.
, chứng minh được AK ^ BC.
Áp dụng cách làm tương tự 4A suy ra ĐPCM
Trã lời dùm