Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔAEB∼ΔAFC(g-g)
b) Ta có: ΔAEB∼ΔAFC(cmt)
nên \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{BAC}\) chung
Do đó: ΔAEF∼ΔABC(c-g-c)

a) Xét \(\Delta AEB\) và \(\Delta AFC\) có:
\(\widehat{AEB}=\widehat{AFC}=90^0\)
\(\widehat{A}\) chung
suy ra: \(\Delta AEB~\Delta AFC\) (g.g)
\(\Rightarrow\)\(\frac{AE}{AF}=\frac{AB}{AC}\) \(\Rightarrow\)\(AF.AB=AE.AC\)
b) \(\frac{AE}{AF}=\frac{AB}{AC}\)\(\Rightarrow\)\(\frac{AE}{AB}=\frac{AF}{AC}\)
Xét \(\Delta AEF\)và \(\Delta ABC\) có:
\(\frac{AE}{AB}=\frac{AF}{AC}\) (cmt)
\(\widehat{A}\) chung
suy ra: \(\Delta AEF~\Delta ABC\) (c.g.c)
\(\Rightarrow\) \(\widehat{AEF}=\widehat{ABC}\)
c) \(\Delta AEF~\Delta ABC\)
\(\Rightarrow\)\(\frac{S_{ABC}}{S_{AEF}}=\left(\frac{AB}{AE}\right)^2=\left(\frac{3}{6}\right)^2=\frac{1}{4}\)
\(\Rightarrow\)\(S_{ABC}=4S_{AEF}\)
Gửi các bạn lời giải 1 bài tương tự
https://youtu.be/mjiZSkISHgA

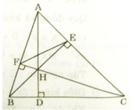
( AF/FB ).(BD/DC).(CE/EA)= AF/AE. BD/FB . CE/DC
sau đó dựa vào các tam giác AEB, BFD,DCE cùng đồng dạng với tam giác ABC

Hướng dẫn làm:
(a) Chứng minh ΔABE∼ΔACF→AEAF=ABAC→ΔAEF∼ΔABC
(b) Chứng minh BH.BE=BD.BC và CH.CF=CD.BC, từ đó suy ra điều phải chứng minh.
(c) Chứng minh ΔBHD∼ΔADC, từ đó ta có tỉ số BDHD=ADDC↔AD.HD=BD.DC
Đặt BD=x thì DC=BC−x
Khi đó 4AD.HD=x(BC−x)=−4x2+4BC.x−BC2+BC2=−(2x−BC)2+BC2≤BC2
(d) Chứng minh AKIˆ=AEIˆ
Sau đó chứng minh ΔEIA∼ΔEQH và suy ra AEIˆ=HEQˆ=HKQˆ
Đúng nha nguyễn ngọc khánh vy
(a) Chứng minh ΔABE∼ΔACF→AEAF=ABAC→ΔAEF∼ΔABC
(b) Chứng minh BH.BE=BD.BC và CH.CF=CD.BC, từ đó suy ra điều phải chứng minh.
(c) Chứng minh ΔBHD∼ΔADC, từ đó ta có tỉ số BDHD=ADDC↔AD.HD=BD.DC
Đặt BD=x thì DC=BC−x
Khi đó 4AD.HD=x(BC−x)=−4x2+4BC.x−BC2+BC2=−(2x−BC)2+BC2≤BC2
(d) Chứng minh AKIˆ=AEIˆ
Sau đó chứng minh ΔEIA∼ΔEQH và suy ra AEIˆ=HEQˆ=HKQˆ
Mình đúng nha nguyễn ngọc khánh vy

#muon roi ma sao con
a, Xét tam giác BEF và tam giác DEA ta có :
^BEF = ^DEA ( đ.đ ) vì AD // BC ( ABCD là hình bình hành )
\(\frac{AE}{EF}=\frac{DE}{BE}\) do AD // BC ( theo định lí Ta lét ) (1)
Vậy tam giác BEF ~ tam giác DEA ( c.g.c )
b, Xét tam giác EGD và tam giác EAB ta có :
^GED = ^EAB ( đ.đ )
\(\frac{AE}{EG}=\frac{BE}{ED}\)AB // DG ( theo định lí Ta lét ) (2)
Vậy tam giác EGD ~ tam giác EAB ( c.g.c )
\(\Rightarrow\frac{EG}{EA}=\frac{ED}{EB}\Rightarrow EG.EB=ED.EA\)( đpcm )
c, Từ (2) ta có : \(\frac{AE}{EG}=\frac{BE}{ED}\Rightarrow\frac{EG}{AE}=\frac{ED}{BE}\)( 3 )
Từ (1) ; (3) ta có : \(\frac{AE}{EF}=\frac{EG}{AE}=\frac{ED}{BE}\Rightarrow AE^2=EG.EF\)
a, Xét tam giác AEB và tam giác AFC ta có
^AEB = ^AEC = 900
^A _ chung
Vậy tam giác AEB ~ tam giác AFC ( g.g )
\(\Rightarrow\frac{AE}{AF}=\frac{AB}{AC}\)( tỉ số đồng dạng ) \(\Rightarrow AE.AC=AB.AF\)

a: Xét ΔAEB vuông tại E và ΔAFC vuông tại F có
góc A chung
=>ΔAEB đồng dạng với ΔAFC
=>AE/AF=AB/AC
=>AE*AC=AB*AF
b: AE/AF=AB/AC
=>AE/AB=AF/AC
=>ΔAEF đồng dạng với ΔABC
=>góc AEF=góc ABC
c: ΔAEF đồng dạng với ΔABC
=>\(\dfrac{S_{AEF}}{S_{ABC}}=\dfrac{1}{4}\)
=>\(S_{ABC}=4\cdot S_{AEF}\)

a) Xét ΔAEB và ΔAFC có:
∠AEB = ∠AFC = 90o (gt)
∠A chung
Vậy ΔAEB ∼ ΔAFC (g.g)
![]()
b) Xét ΔAEF và ΔABC có
∠A chung
AF.AB = AE.AC (Cmt)
⇒ ΔAEF ∼ ΔABC (c.g.c)
⇒ ∠AEF = ∠ABC
c) ΔAEF ∼ ΔABC (cmt)

![]()
![]()
![]()
![]()
![]()
![]()
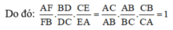

a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc A chung
=>ΔABE đồng dạng với ΔACF
b: ΔABE đồng dạng với ΔACF
=>AE/AF=AB/AC
=>AE/AB=AF/AC và AE*AC=AB*AF
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
=>ΔAEF đồng dạng với ΔABC
jjjjjjjjjjjjjj