Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tổng quát cho câu 2 là định lí Ptolemy, như sau: Cho \(ABCD\) nội tiếp bất kì. Khi đó \(AC.BD=AB.CD+AD.BC\).
A B C D E
CM: Vẽ \(E\in AC\) sao cho \(\widehat{ABD}=\widehat{EBC}\).
Khi đó có hai tam giác sau đồng dạng \(ABD\) và \(EBC\), \(ABE\) và \(DBC\).
Suy ra tỉ lệ cạnh: \(\frac{AD}{EC}=\frac{BD}{BC}\) và \(\frac{AB}{DB}=\frac{AE}{DC}\).
Hay \(AD.BC=BD.EC\) và \(AB.DC=AE.DB\)
Cộng lại: \(AB.CD+AD.BC=BD\left(AE+EC\right)=AC.BD\)

A B C D I R H K J M N O
Gọi M, N lần lượt là chân đường cao hạ từ B,C xuống AC,AB
Ta có \(DH.DA=DB.DC\)(1)
Để chứng minh K là trực tâm tam giác IBC ta chứng minh \(DK.DJ=DB.DC\)hay \(DK.DJ=DH.DA\)
Ta có NC,NA lần lượt là phân giác trong và phân giác ngoài của \(\widehat{MND}\)nên
\(\frac{HK}{HD}=\frac{NK}{ND}=\frac{AK}{AH}\)
\(\Rightarrow AK.HD=AD.HK\)
\(\Leftrightarrow HD\left(AD-DK\right)=AD\left(DK-DH\right)\)
\(\Leftrightarrow2.AD.DH=DK\left(DA+DH\right)\)
\(\Leftrightarrow2.AD.DH=2.DK.DJ\)
\(\Rightarrow AD.DH=DK.DJ\left(2\right)\)
Từ (1) và (2) ta có\(DK.DJ=DH.DA\)
=> K là trực tâm của tam giác IBC

a) Gọi F là điểm đối xứng với A qua O ⇒ AF là đường kính của (O)
Ta có ACF = ABF = 90o (góc nội tiếp chắn nửa đường tròn) ⇒ AC ⊥ CF , AB ⊥ BF
Mà BH ⊥ AC, CH ⊥ AB ⇒ CF // BH, BF // HC
Suy ra BHCF là hình bình hành ⇒ Trung điểm M của BC cũng là trung điểm của HF.
⇒ OM là đường trung bình của ∆ AHF ⇒ AH = 2OM


Bài 1:
b)
chứng minh EDCB là tgnt => góc AED = góc ACB
từ đó, chứng minh tam giác AED đồng dạng ACB (gg)
=> DE / BC = AD / AB
tam giác ADB vuông tại A => AD / AB = cotg A = cotg 45 = 1
c)
kẻ tiếp tuyến tại Ax của (O) (Ax thuộc nửa mp bờ AC chứa B)
góc xAB = ACB = AED
=> DE // Ax
Mà Ax vuông góc với OA nên OA vuông góc với DE. (đpcm)

Cho △ABC nhọn (AB<AC) nội tiếp (O), 2 đường cao BD và CE cắt nhau tại H
a/ Chứng minh : B,C,D,E cùng nằm trên một đường tròn .Xác định tâm M của đường tròn này.
b/ Chứng minh : OM // AH
c/ Chứng minh : AB.AE = AC.AD
d/ Gọi K là điểm đối xứng của H qua M .

A B C O E F K I J H M N S T L
c) AT là đường kính của (O), dễ thấy H,K,T thẳng hàng, gọi TH cắt (O) lần nữa tại S, ta được ^ASH = 900
Ta có A,E,H,F,S cùng thuộc đường tròn đường kính AH, suy ra:
(ES,EF) = (AS,AB) = (SC,SB), (SF,SE) = (BS,BC) do đó \(\Delta\)SFE ~ \(\Delta\)SBC
Vì K,L là trung điểm của BC,EF nên \(\Delta\)SFL ~ \(\Delta\)SBK, suy ra \(\Delta\)SFB ~ \(\Delta\)SLK, (KS,KL) = (BS,BA) (1)
Lại có: \(\frac{MF}{MB}=\frac{HF}{HB}=\frac{HE}{HC}=\frac{NE}{NC}\), \(\Delta\)SEC ~ \(\Delta\)SFB, suy ra \(\Delta\)SMN ~ \(\Delta\)SBC
Tương tự như trên, ta thu được (KS,KI) = (BS,BA) (2)
Từ (1);(2) suy ra K,I,L thẳng hàng. Mặt khác K,L,J thẳng hàng vì chúng cách đều E,F.
Do vậy I,J,K thẳng hàng.
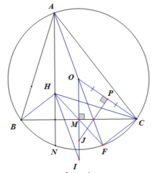
b) Vì AHIO là hình bình hành nên OI = AH = 2OM
Gọi P là trung điểm OC ⇒ PJ là trung trực OC ⇒ PJ ⊥ OC.
Có OM là trung trực BC ⇒ OM ⊥ BC. Suy ra
Δ O J P ~ Δ O C M ( g . g ) ⇒ O J O C = O P O M ⇒ O J . O M = O C . O P ⇒ O J .2 O M = O C .2 O P ⇒ O J . O I = O C . O C = R 2