Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{a) Xét tứ giác BEFC có:}\)
\(\text{∠BEC = 90 o (CE là đường cao)}\)
\(\text{∠BFC = 90 ^0 (BF là đường cao)}\)
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc vuông
=> Tứ giác BEFC là tứ giác nội tiếp
\(\text{Xét tứ giác AEHF có:}\)
\(\text{∠AEH = 90 o (CE là đường cao)}\)
\(\text{∠AFH = 90 o (BF là đường cao)}\)
=> ∠AEH + ∠AFH = 180^ o
=> Tứ giác AEHF là tứ giác nội tiếp.
\(\text{b) Xét ΔSBE và ΔSFC có:}\)
\(\text{∠FSC là góc chung}\)
\(\text{∠SEB = ∠SCF (Tứ giác BEFC là tứ giác nội tiếp)}\)
=> ΔSBE ∼ ΔSFC (g.g)
\(\Rightarrow\frac{SB}{SF}\)=\(\frac{SE}{SC}\)\(\Rightarrow\text{SE.SF = SB.SC (1)}\)
\(\text{Xét ΔSMC và ΔSNB có:}\)
\(\text{∠ NSC là góc chung}\)
\(\text{∠ SCM = ∠SNB (Hai góc nội tiếp cùng chắn cung MB)}\)
=> ΔSMC ∼ ΔSBN (g.g)
\(\Rightarrow\frac{SM}{SB}\)=\(\frac{SC}{SN}\Rightarrow\text{SM.SN = SB.SC (2)}\)
Từ (1) và (2) => SE.SF = SM.SN
\(\text{c) Ta có:}\)
\(\hept{\begin{cases}\widehat{KAE}=\widehat{KCB}\left(\text{2 GÓC NỘI TIẾP CÙNG CHẮN CUNG KB}\right)\\\widehat{HAE}=\widehat{BFM}\left(\text{TỨ GIÁC AEHF LÀ TỨ GIÁC NỘI TIẾP}\right)\\\widehat{KCB}=\widehat{BFM}\left(\text{TỨ GIÁC BEFC LÀ TỨ GIÁC NỘI TIẾP}\right)\end{cases}}\)
=> ∠KAE = ∠HAE
=> AE là tia phân giác của góc ∠KAH
\(\text{Mà AE cũng là đường cao của tam giác KAH}\)
=> ΔKAH cân tại A
=> AE là đường trung tuyến của ΔKAH
=> E là trung điểm của KH hay K và H đối xứng nhau qua AB
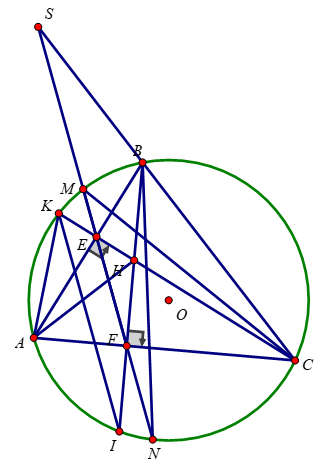
\(\text{d) Tia BF cắt đường tròn (O) tại J}\)
∠KJB = ∠KCB (2 góc nội tiếp cùng chắn cung KB)
∠KCB = ∠EFH (tứ giác BEFC là tứ giác nội tiếp )
=> ∠KJB = ∠EFH
Mà 2 góc này ở vị trí so le trong
=> KJ // EF
KI // EF (gt)
=> I ≡ J
=> H, F, J thẳng hàng
HÌNH THÌ VÀO XEM THỐNG KÊ HỎI ĐÁP NHA
BÀI LÀM ĐÚNG MÀ SAO CÓ NGƯỜI K SAI TÔI ĐẢM BẢO BÀI NÀY ĐÚNG 100%

1). Tam giác ABF và tam giác ACE ần lượt cân tại F, E và
F B A ^ = E C A ^ = A ^ 2 ⇒ Δ A B F ∽ Δ A C E .
2). Giả sử G là giao điểm của BE và CF.
Ta có G F G C = B F C E = A B A C = D B D C ⇒ G D ∥ F B , và F B ∥ A D ta có G ∈ A D .
3). Chứng minh B Q G ^ = Q G A ^ = G A E ^ = G A C ^ + C A E ^ = G A B ^ + B A F ^ = G A F ^ , nên AGQF nội tiếp, và Q P G ^ = G C E ^ = G F Q ^ , suy ra tứ giác FQGP nội tiếp.
1) Chứng minh rằng tam giác \( A B F \) đồng dạng với tam giác \( A C E \):
- Tam giác \(ABF\) và \(ACE\) có:
+ Góc \(A\) chung.
+ Góc \(BAF\) bằng góc \(CAE\) (vì \(AD\) là phân giác của góc \(BAC\) và \(CF\), \(BE\) song song với \(AD\)).
Do đó, tam giác \(ABF\) đồng dạng với tam giác \(ACE\) (theo trường hợp góc-góc).
2) Chứng minh rằng các đường thẳng \(BE\), \(CF\), \(AD\) đồng quy:
- Gọi \(G\) là giao điểm của \(BE\) và \(CF\).
- \(AD\) là phân giác góc \(BAC\), và \(BE\), \(CF\) song song với \(AD\). Do đó, \(G\) cũng nằm trên phân giác \(AD\).
- Vậy \(BE\), \(CF\), \(AD\) đồng quy tại \(G\).
3) Chứng minh rằng các điểm \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn:
- Gọi đường tròn ngoại tiếp tam giác \(GEC\) là \(\omega\).
- \(QE\) cắt \(\omega\) tại \(P\) khác \(E\), vậy \(P\) nằm trên đường tròn \(\omega\).
- \(GQ\) song song với \(AE\), và \(AE\) là đường kính của \(\omega\) (vì \(E\) là trung điểm của \(AC\) và \(G\) nằm trên phân giác của \(BAC\)). Do đó, \(GQ\) là dây cung của \(\omega\).
- \(PF\) là tiếp tuyến của \(\omega\) tại \(P\) (vì \(QE\) là tiếp tuyến và \(PF\) là phần kéo dài của \(QE\)).
- Góc \(PGF\) bằng góc \(GAC\) (cùng chắn cung \(GC\) của \(\omega\)).
- \(AF\) là trung trực của \(AB\), nên \(ABF\) là tam giác cân tại \(A\). Do đó, góc \(AFB\) bằng góc \(ABF\).
- Góc \(ABF\) bằng góc \(GAC\) (do đồng dạng của tam giác \(ABF\) và \(ACE\)).
- Vậy, góc \(PGF\) bằng góc \(AFB\). Do đó, \(A\), \(P\), \(G\), \(Q\), \(F\) cùng thuộc một đường tròn.


2) Theo 1). dễ thấy Δ B F A ∽ Δ B N P ⇒ Δ B N F ∽ Δ B P A ⇒ B N B P = F N A P (1).
Tương tự Δ C M E ∽ Δ C P A ⇒ C M C P = E M A P (2).
Từ (1) và (2), ta có B N C M ⋅ C P B P = F N E M và theo giả thiết F N E M = B N C M , suy ra C P = B P ⇒ A D là phân giác góc B A C ^ .

\(\text{a) Ta có:}\)
∠BFC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AFC = 90o
∠BEC = 90o (góc nội tiếp chắn nửa đường tròn)=> ∠AEC = 90o
Tứ giác AEHF có:
∠AFC = 90o
∠AEC = 90o
=>∠AFC + ∠AEC = 180o
=> AEHF là tứ giác nội tiếp
b) ∠AFH = 90o => AH là đường kính đường tròn ngoại tiếp tứ giác AEHF
\(\text{Do đó trung điểm I của AH là tâm đường tròn ngoại tiếp tứ giác AEHF}\)
=> Bán kính đường tròn ngoại tiếp tứ giác AEHF là R = AI = \(\frac{AH}{2}\) = 2cm
Ta có: ∠BAC = 60o
=> ∠FIE = 2∠BAC = 120o (Góc nội tiếp bằng \(\frac{1}{2}\) góc ở tâm cùng chắn một cung)
=> Số đo ∠EHF = 120o
Diện tích hình quạt IEHF là:
\(S=\frac{\pi R^2N}{360}=\frac{\pi.2^2.120}{360}=\frac{4\pi}{3}\left(ĐVDT\right)\)
\(\text{c) Xét tam giác ABC có: }\)
BE và CF là các đường cao
BE giao với CF tại H
=> H là trực tâm tam giác ABC
=>AH ⊥ BC hay ∠ADC = ∠ADB = 90o
Xét tứ giác BEFC có:
∠BFC = ∠BEC = 90o
=> 2 đỉnh E, F cùng nhìn cạnh BC dưới 1 góc bằng nhau
=> BEFC là tứ giác nội tiếp
=> ∠HFE = ∠BEC ( 2 góc nội tiếp cùng chắn cung EC) (1)
Xét tứ giác BFHD có:
∠BFH = ∠HDB = 90o
=>∠BFH + ∠HDB = 180o
=> Tứ giác BFHD là tứ giác nội tiếp ( tổng 2 góc đối bằng 180o)
=> ∠DFH = ∠BEC ( 2 góc nội tiếp cùng chắn cung HD) (2)
Từ (1) và (2) = > ∠HFE = ∠DFH
=> FH tia phân giác của góc ∠DFE
d) Tam giác OFB cân tại O => ∠OFB = ∠FBO
Tam giác BFC vuông tại F => ∠FBO + ∠HCD = 90o
=> ∠OFB + ∠HCD = 90o (*)
\(\hept{\begin{cases}\Delta FIH\text{CÂN TẠI I}\\\widehat{IHF}=\widehat{DHC}\left(\text{ĐỐI ĐỈNH}\right)\\\Delta HDC\text{VUÔNG TẠI D}\Rightarrow\widehat{DHC}+\widehat{HDC}=90^0\end{cases}}\Rightarrow\widehat{IFH}+\widehat{HDC}=90^0\)
Từ (*) và (**) => ∠OFB = ∠IFH
=> ∠OFB + ∠OFH = ∠IFH + ∠OFH <=> ∠BFC = ∠FIO <=> ∠FIO) = 90o
Vậy FI là tiếp tuyến của (O)
Chứng minh tương tự EI là tiếp tuyến của (O)
Mà I là trung điểm của AH
=> Tiếp tuyến của (O) tại E và F và AH đồng quy tại 1 điểm.
HÌNH THÌ VÀO THỐNG KÊ HỎI ĐÁP CỦA MIK NHA
VCN JACK trả lời cuc64 kì đ luôn . đ là chất

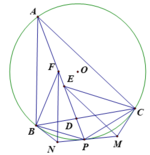
1). Gọi AD cắt (O) tại P khác A
Ta có P C M ^ = P A C ^ (góc tạo bởi tiếp tuyến và dây cung) = P E M ^ (góc đồng vị do E M ∥ A C );
Suy ra tứ giác ECMP nội tiếp. Từ đó suy ra M P C ^ = M E C ^ = E C A ^ = C A P ^ ⇒ PM tiếp xúc (O)
Tương tự PN tiếp xúc (O), suy ra MN tiếp xúc (O) tại P.

\(\widehat{BKC}=\widehat{BHC}\left(=90^0\right)\) nên HKBC nội tiếp đường tròn

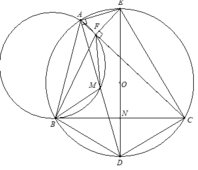
1). Ta có góc nội tiếp bằng nhau B D M ^ = B C F ^ ( 1 ) và B M A ^ = B F A ^ suy ra 180 0 − B M A ^ = 180 0 − B F A ^ hay B M D ^ = B F C ^ (2).
Từ (1) và (2), suy ra Δ B D M ~ Δ B C F (g - g).
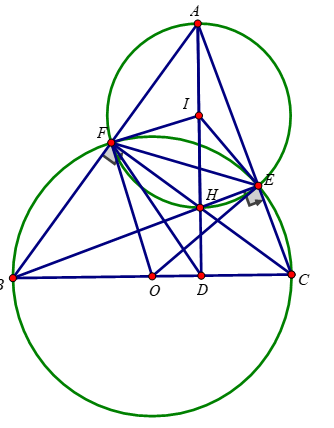
a) Dễ thấy tứ giác BDHF có \(\widehat{BDH}+\widehat{BFH}=90^o+90^o=180^o\)
\(\Rightarrow\) Tứ giác BDHF nội tiếp (dhnb)
Tứ giác BCEF có \(\widehat{BEC}=\widehat{BFC}\left(=90^o\right)\)
\(\Rightarrow\) Tứ giác BCEF nội tiếp (dhnb)
b) Tứ giác BDHF nội tiếp (cmt) \(\Rightarrow\widehat{DFH}=\widehat{DBH}\) hay \(\widehat{DFC}=\widehat{EBC}\)
Tứ giác BCEF nội tiếp (cmt) \(\Rightarrow\widehat{EFC}=\widehat{EBC}\)
Từ đó ta có \(\widehat{DFC}=\widehat{EFC}\left(=\widehat{EBC}\right)\)
\(\Rightarrow\) FC là tia phân giác \(\widehat{EFD}\) (đpcm)
c) Ta có \(\widehat{DFC}=\widehat{EFC}\) (cmt) \(\Rightarrow90^o-\widehat{DFC}=90^o-\widehat{EFC}\)\(\Rightarrow\widehat{AFE}=\widehat{BFD}\)
Mà \(\widehat{AFE}=\widehat{BFM}\) (2 góc đối đỉnh) \(\Rightarrow\widehat{BFD}=\widehat{BFM}\)
\(\Rightarrow\) FB là tia phân giác của \(\widehat{DFM}\)
Theo tính chất đường phân giác trong tam giác DFM, ta có \(\dfrac{FD}{FM}=\dfrac{BD}{BM}\)
Lại có FC là tia phân giác \(\widehat{EFD}\) (cmt), theo tính chất đường phân giác của góc ngoài của tam giác, ta có \(\dfrac{FD}{FM}=\dfrac{CD}{CM}\)
Do đó, ta có \(\dfrac{BD}{BM}=\dfrac{CD}{CM}\)\(\Rightarrow\dfrac{BD}{CD}=\dfrac{BM}{CM}\) (1)
\(\Delta MAC\) có \(BI//AC\left(gt\right)\) nên \(\dfrac{BI}{AC}=\dfrac{BM}{CM}\) (2) (định lý Ta-lét)
\(\Delta ACD\) có \(BK//AC\left(gt\right)\) nên \(\dfrac{BK}{AC}=\dfrac{BD}{CD}\) (3) (hệ quả định lý Ta-lét)
Từ (1), (2), (3) \(\Rightarrow\dfrac{BI}{AC}=\dfrac{BK}{AC}\Rightarrow BI=BK\)
\(\Rightarrow\) B là trung điểm IK \(\Rightarrow\) HB là trung tuyến của \(\Delta HIK\)
Mặt khác AC//IK (gt), lại có \(BE\perp AC\) nên \(BE\perp IK\), từ đó suy ra HB là đường cao của \(\Delta HIK\)
\(\Delta HIK\) có HB vừa là đường cao vừa là trung tuyến \(\Rightarrow\Delta HIK\) cân tại H (đpcm)