Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình làm câu đầu tiên nhé :)
a) Xét tam giác ABM và tam giác DMC có :
BM = CM ( gt )
\(\widehat{AMB}=\widehat{DMC}\)
AM = DM ( gt )
\(\Rightarrow\)\(\Delta AMB=\Delta DMC\left(c-g-c\right)\)
\(\Rightarrow\)\(\widehat{BAM}=\widehat{DCM}\)( 2 góc tương ứng bằng nhau )
Mà 2 góc này ở vị trí so le trong nên suy ra AB // CD

Xét ΔDCM và ΔABM có:
AM = MD ( GT )
BM = BC (AM là đường trung tuyến của ΔABC tại đỉnh A)
góc BMA = góc DMC ( hai góc đối đỉnh)
=> ΔDMC = Δ ABM (c.g.c)
=> Góc BAM = Góc MDC ( hai góc tương ứng)
mà Góc BAM và Góc MDC nằm ở vị trí so le trong
=> AB\\CD
b) xét ΔAKM và Δ DFM có
góc KMA = góc DMF ( 2 góc đối đỉnh)
góc BAM = góc MDC (cmt)
AM = MD ( GT )
=> ΔAKM = ΔDFM (g.c.g)
=> MK = MF ( 2 cạnh tương ứng)
=> M là trung điểm của KF
Học tốt

a: Xét ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//DC
b: Xét ΔKMB và ΔFMC có
góc MBK=góc MCK
MB=MC
góc KMB=góc FMC
=>ΔKMB=ΔFMC
=>MK=MF
=>M là trung điểm của KF

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )

a, xét t.giác AMB và t.giác DMC có:
AM=DM(gt)
\(\widehat{AMB}\)=\(\widehat{DMC}\)(vì đối đỉnh)
CM=BM(gt)
=>t.giác AMB=t.giác DMC(c.g.c)
b,đề bài bị thiếu

Bạn tự vẽ hình nha![]()
a.
Xét tam giác ABO và tam giác CDO có:
AO = CO (BO là trung truyến của tam giác ABC)
AOB = COD (2 góc đối đỉnh)
BO = DO (gt)
=> Tam giác ABO = Tam giác CDO (c.g.c)
=> BAO = DCO (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AB // CD.
b.
BO là trung tuyến của tam giác ABC
=> O là trung điểm của AC
=> AO = CO = \(\frac{1}{2}AC\) (1)
- BO = DO (gt) => CO là trung tuyến của tam giác BCD
- BM = CM (M là trung điểm của BC) => DM là trung tuyến của tam giác BCD
=> I là giao điểm của 2 đường trung tuyến CO và DM của tam giác BCD
=> I là trọng tâm của tam giác BCD.
=> IO = \(\frac{1}{3}OC\) (2)
Thay (1) vào (2), ta có:
IO = \(\frac{1}{3}OC=\frac{1}{3}\times\frac{1}{2}AC=\frac{1}{6}AC\)
\(\Rightarrow AC=6\times IO\)
c.
AB // CD
=> EBM = DCM (2 góc so le trong)
Xét tam giác EBM và tam giác DCM có:
EBM = DCM (chứng minh trên)
BM = CM (M là trung điểm của BC)
BME = CMD (2 góc đối đỉnh)
=> Tam giác EBM = Tam giác DCM (g.c.g)
=> BE = CD (2 cạnh tương ứng)
mà CD = AB (tam giác ABO = tam giác CDO)
=> BE = AB.
Chúc bạn học tốt![]()


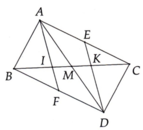
a: Xét ΔAMB và ΔDMC có
MB=MC
\(\widehat{AMB}=\widehat{DMC}\)
MA=MD
Do đó: ΔAMB=ΔDMC
Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
Suy ra: AB//CD
b: Xét ΔCBD có
M là trung điểm của BC
F là trung điểm của DC
Do đó: MF là đường trung bình
=>MF//BD
=>MF//AC
hay MK//AC
Xét ΔBAC có
M là trung điểm của BC
MK//AC
DO đó: K là trung điểm của BA
Xét tứ giác BKCF có
BK//CF
BK=CF
Do đó: BKCF là hình bình hành
Suy ra: Hai đường chéo BC và KF cắt nhau tại trung điểm của mỗi đường
hay M là trung điểm của KF