Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

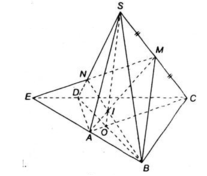
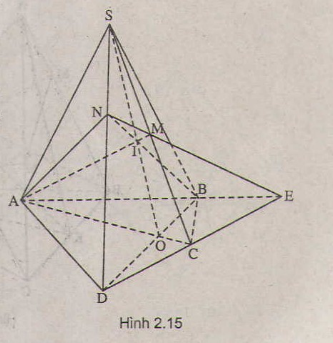
a) + Trong mp(ABCD), AB cắt CD tại E.
E ∈ AB ⊂ (MAB) ⇒ E ∈ (MAB) ⇒ ME ⊂ (MAB)
E ∈ CD ⊂ (SCD) ⇒ E ∈ (SCD)
Mà M ∈ SC ⊂ (SCD)
⇒ ME ⊂ (SCD).
+ Trong mp(SCD), EM cắt SD tại N.
Ta có:
N ∈ SD
N ∈ EM ⊂ mp(MAB)
Vậy N = SD ∩ mp(MAB)
b) Chứng minh SO, MA, BN đồng quy:
+ Trong mặt phẳng (SAC) : SO và AM cắt nhau.
+ trong mp(MAB) : MA và BN cắt nhau
+ trong mp(SBD) : SO và BN cắt nhau.
+ Qua AM và BN xác định được duy nhất (MAB), mà SO không nằm trong mặt phẳng (MAB) nên AM; BN; SO không đồng phẳng.
Vậy SO, MA, BN đồng quy.

Câu 1:
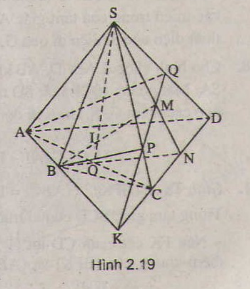
a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ
Câu 2:
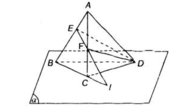
a) Trong (ABCD) gọi M = AE ∩ DC => M ∈ AE, AE ⊂ ( C'AE) => M ∈ ( C'AE). Mà M ∈ CD => M = DC ∩ (C'AE)
b) Chứng minh M ∈ (SDC), trong (SDC) : MC' ∩ SD = F. Chứng minh thiết diện là AEC'F
Câu 3:
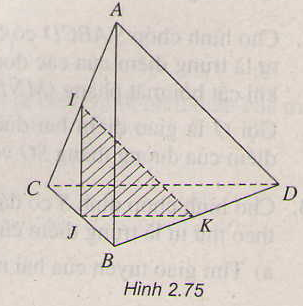
a) Chứng minh E, N là hai điểm chung của mặt phẳng (PMN) và (BCD)
b) EN ∩ BC = Q. Chứng minh Q là điểm cần tìm
Câu 4:
a) Chứng minh I, K là hai điểm chung của (BIC) và (AKD)
b) Gọi P = CI ∩ DN và Q = BI ∩ DM, chứng minh PQ là giao tuyến cần tìm
Câu 5:
a) Trong mặt phẳng (α) vì AB và CD không song song nên AB ∩ DC = E
=> E ∈ DC, mà DC ⊂ (SDC)
=> E ∈ ( SDC). Trong (SDC) đường thẳng ME cắt SD tại N
=> N ∈ ME mà ME ⊂ (MAB)
=> N ∈ ( MAB). Lại có N ∈ SD => N = SD ∩ (MAB)
b) O là giao điểm của AC và BD => O thộc AC và BD, mà AC ⊂ ( SAC)
=> O ∈( SAC), BD ⊂ (SBD) , O ∈ (SBD)
=> O là một điểm chung của (SAC) và (SBD), mặt khác S cũng là điểm chung của (SAC) và (SBD) => (SAC) ∩ (SBD) = SO
Trong mặt phẳng (AEN) gọi I = AM ∩ BN thì I thuộc AM và I thuộc BN
Mà AM ⊂ (SAC) => I ∈ (SAC), BN ⊂ ( SBD) => I ∈ (SBD). Như vậy I là điểm chung của (SAC) và (SBD) nên I thuộc giao tuyến SO của (SAC) và (SBD) tức là S, I, O thẳng hàng hay SO, AM, BN đồng quy

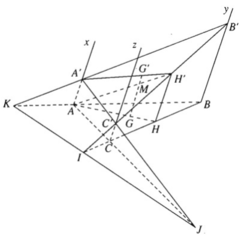
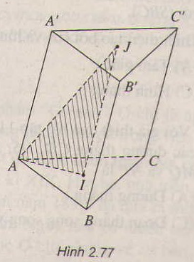
a) CC′ // BB′ ⇒ ΔICC′ ∼ ΔIBB′
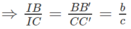
CC′ // AA′ ⇒ ΔJCC′ ∼ ΔJAA′
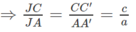
AA′ // BB′ ⇒ ΔKAA′ ∼ ΔKBB′
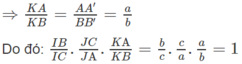
b) Gọi H và H’ lần lượt là trung điểm của các cạnh BC và B’C’. Vì HH’ là đường trung bình của hình thang BB’CC’ nên HH′ // BB′.
Mà BB′ // AA′ suy ra HH′ // AA′
Ta có: G ∈ AH và G′ ∈ A′H′ và ta có:
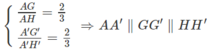
c) AH′ ∩ GG′ = M ⇒ GG′ = G′M + MG
Ta có: G′M // AA′ ⇒ ΔH′G′M ∼ ΔH′A′A
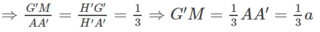
MG // HH′ ⇒ ΔAMG ∼ ΔAH′H
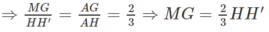
Mặt khác HH’ là đường trung bình của hình thang BB’CC’ nên
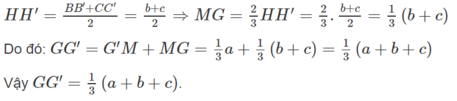

Đáp án C
Do a là giao điểm của ( α ) và ( β ) nên a và d cắt nhau.

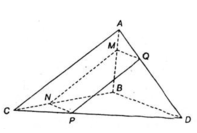
a) + (α) // AC
⇒ Giao tuyến của (α) và (ABC) là đường thẳng song song với AC.
Mà M ∈ (ABC) ∩ (α).
⇒ (ABC) ∩ (α) = MN là đường thẳng qua M, song song với AC (N ∈ BC).
+ Tương tự (α) ∩ (ABD) = MQ là đường thẳng qua M song song với BD (Q ∈ AD).
+ (α) ∩ (BCD) = NP là đường thẳng qua N song song với BD (P ∈ CD).
+ (α) ∩ (ACD) = QP.
b)Ta có:
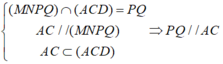
Suy ra, tứ giác MNPQ có các cạnh đối song song với nhau nên tứ giác MNPQ là hình bình hành.

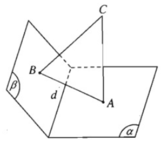
Hai mặt phẳng (α) và (β) không thể trùng nhau vì nếu chúng trùng nhau thì từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với một mặt phẳng, điều đó là vô lí.
Mặt khác (α) và (β) cũng không song song với nhau.
Vì nếu (α) // (β), thì từ CB ⊥ (β) ta suy ra CB ⊥ (α)
Như vậy từ một điểm C ta dựng được hai đường thẳng CA, CB cùng vuông góc với (α), điều đó là vô lí.
Vậy (α) và (β) là hai mặt phẳng không trùng nhau, không song song với nhau và chúng phải cắt nhau theo giao tuyến d, nghĩa là d = (α) ∩ (β)
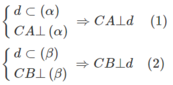
Từ (1) và (2) suy ra d ⊥ (ABC).

a) E ∈ AB mà AB ⊂ (ABC)
⇒ E ∈ (ABC)
F ∈ AC mà AC ⊂ (ABC)
⇒ F ∈ (ABC)
Đường thẳng EF có hai điểm E, F cùng thuộc mp(ABC) nên theo tính chất 3 thì EF ⊂ (ABC).
b) I ∈ BC mà BC ⊂ (BCD) nên I ∈ (BCD) (1)
I ∈ EF mà EF ⊂ (DEF) nên I ∈ (DEF) (2)
Từ (1) và (2) suy ra I là điểm chung của hai mặt phẳng (BCD) và (DEF).

a) Trong (SCD) kéo dài SM cắt CD tại N, Chứng minh N thuộc (SBM)
b) (SBM) ≡ (SBN). Giao tuyến cần tìm là SO
c) Trong (SBN) ta có MB giao SO tại I
d) Trong (ABCD) , ta có AB giao CD tại K, Trong (SCD), ta có KQ giao SC tại P
Từ đó suy ra được giao tuyến của hai mặt phẳng (SCD) và (ABM) là KQ.

Lời giải:
Gọi $K$ là giao điểm của đường thẳng $a$ với $AB$ thì $A'K\subset (A',a)$
Ta thấy: $K\in AB; A'\in SA\Rightarrow A'K\subset (SAB)$
Do đó $A'K$ là giao tuyến của $(A',a)$ và $(SAB)$
Giao tuyến với các mặt phẳng $(SAC,SBC)$ bạn thực hiện tương tự.