Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác ABM và tam giác DCM có:
+, BM = MC ( AM là đường trung tuyến của tam giác ABC )
+, Góc AMB = góc DMC ( 2 góc đối đỉnh )
+, AM = MD ( gt )
=> tam giác ABM = tam giác DCM ( c.g.c )
=> AB = CD ( 2 cạnh tương ứng )
=> góc BAM = góc CDM ( 2 góc tương ứng )
Mà 2 góc này ở vị trí so le trong
=> AB // CD ( đpcm )

cho tam giác ABC vuông tại A có AB=3cm,BC=5cm. Gọi N là trung điểm BC, trên tia đối N lấy điếm D sao cho ND=NA
a)C/m: tam giác ACN= tam giác DBN
b)Tính BD
c)Gọi M là trung điểm AB. C/m: tam giác MDC cân
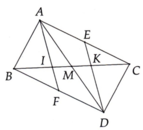
d)MD cắt BC tại H, gọi I là trung điểm của AC, DI cắt BC tại K. C/m: tam giác HBD= tam giác KCA
e)AH cắt BD tại E. C/m: AE+DE>6NH
DS: ai giỏi thì giảng cho ông ay nha

Xét ∆ABM và ∆CDM ta có :
AM = MD
BM = MC
AMB = CMD ( đối đỉnh)
=> ∆ABM = ∆CDM(c.g.c)
=> BAM = CDM ( tg ứng )
Mà 2 góc này ở vị trí so le trong
=> AB//CD
=> AB= CD

Bài 1 : Bài giải
Bài 2 : Bài giải
Bài 3 : Bài giải
Xét 2 tam giác \(\Delta ABI\text{ và }\Delta EBI\) có :
\(BA=BE\) ( gt )
\(BD\) : cạnh chung
\(\widehat{B_1}=\widehat{B_2}\) ( BD là đường phân giác của \(\widehat{B}\) )
\(\Rightarrow\text{ }\Delta ABD=\Delta EBD\text{ }\left(c.g.c\right)\)
\(\Rightarrow\text{ }AD=DE\text{ }\left(2\text{ cạnh tương ứng }\right)\)
....
Tự làm tiếp nha ! Mình bận rồi !

Mình làm câu đầu tiên nhé :)
a) Xét tam giác ABM và tam giác DMC có :
BM = CM ( gt )
\(\widehat{AMB}=\widehat{DMC}\)
AM = DM ( gt )
\(\Rightarrow\)\(\Delta AMB=\Delta DMC\left(c-g-c\right)\)
\(\Rightarrow\)\(\widehat{BAM}=\widehat{DCM}\)( 2 góc tương ứng bằng nhau )
Mà 2 góc này ở vị trí so le trong nên suy ra AB // CD

Bạn tự vẽ hình nha![]()
a.
Xét tam giác ABO và tam giác CDO có:
AO = CO (BO là trung truyến của tam giác ABC)
AOB = COD (2 góc đối đỉnh)
BO = DO (gt)
=> Tam giác ABO = Tam giác CDO (c.g.c)
=> BAO = DCO (2 góc tương ứng)
mà 2 góc này ở vị trí so le trong
=> AB // CD.
b.
BO là trung tuyến của tam giác ABC
=> O là trung điểm của AC
=> AO = CO = \(\frac{1}{2}AC\) (1)
- BO = DO (gt) => CO là trung tuyến của tam giác BCD
- BM = CM (M là trung điểm của BC) => DM là trung tuyến của tam giác BCD
=> I là giao điểm của 2 đường trung tuyến CO và DM của tam giác BCD
=> I là trọng tâm của tam giác BCD.
=> IO = \(\frac{1}{3}OC\) (2)
Thay (1) vào (2), ta có:
IO = \(\frac{1}{3}OC=\frac{1}{3}\times\frac{1}{2}AC=\frac{1}{6}AC\)
\(\Rightarrow AC=6\times IO\)
c.
AB // CD
=> EBM = DCM (2 góc so le trong)
Xét tam giác EBM và tam giác DCM có:
EBM = DCM (chứng minh trên)
BM = CM (M là trung điểm của BC)
BME = CMD (2 góc đối đỉnh)
=> Tam giác EBM = Tam giác DCM (g.c.g)
=> BE = CD (2 cạnh tương ứng)
mà CD = AB (tam giác ABO = tam giác CDO)
=> BE = AB.
Chúc bạn học tốt![]()


a: Xét ΔNAB và ΔNDC có
NA=ND
\(\widehat{ANB}=\widehat{DNC}\)(hai góc đối đỉnh)
NB=NC
Do đó: ΔNAB=ΔNDC
=>\(\widehat{NAB}=\widehat{NDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: Xét ΔNAC và ΔNDB có
NA=ND
\(\widehat{ANC}=\widehat{DNB}\)(hai góc đối đỉnh)
NC=NB
Do đó: ΔNAC=ΔNDB
=>\(\widehat{NAC}=\widehat{NDB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD