Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔABC có
M là trung điểm của AB
P là trung điểm của BC
Do đó: MP là đường trung bình của ΔBAC
Suy ra: MP//AC và \(MP=\dfrac{AC}{2}=5\left(cm\right)\)
Xét ΔABC có
N là trung điểm của AC
P là trung điểm của BC
Do đó: NP là đường trung bình của ΔABC
Suy ra: NP//AB và \(NP=\dfrac{AB}{2}=2.5\left(cm\right)\)
Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}=5\left(cm\right)\)

a: Ta có: ΔABC vuông tại A
mà AP là đường trung tuyến
nên \(AP=\dfrac{BC}{2}=5\left(cm\right)\)
Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{1}{2}BC\)
=>\(MN=\dfrac{1}{2}\cdot10=5\left(cm\right)\)
b: Xét ΔABC có
N,P lần lượt là trung điểm của CA,CB
=>NP là đường trung bình của ΔABC
=>NP//AB và \(NP=\dfrac{AB}{2}\)
Ta có: NP//AB
M\(\in\)AB
Do đó: NP//AM
ta có: \(NP=\dfrac{AB}{2}\)
\(AM=\dfrac{AB}{2}\)=MB
Do đó; NP=AM=MB
Xét tứ giác AMPN có
AM//NP
AM=NP
Do đó: AMPN là hình bình hành
Hình bình hành AMPN có \(\widehat{MAN}=90^0\)
nên AMPN là hình chữ nhật

Xét tam giác ABC có M và N lần lượt là trung điểm của AB và AC nên MN là đường trung bình của tam giác ABC
Suy ra: MN// BC và
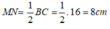
Tương tự, có NP là đường trung bình của tam giác nên: NP // AB
Xét tứ giác MNPB có MN// BC và NP // AB
Suy ra: tứ giác MNPB là bình hành.
Tam giác ABC có đường cao AH = 10cm nên đường cao ứng với cạnh đáy của hình bình hành MNPB là:
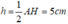
Diện tích hình bình hành MNPB là:
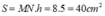
Chọn đáp án C

Bài 2:
D là điểm đối xứng của C qua B nên \(BC=BD\)
Lại có \(AB=BC=10\left(cm\right)\)
\(\Rightarrow AB=\dfrac{CD}{2}\)
Do đó tam giác ADC vuông tại A
Theo định lí Pitago ta có:
\(AD^2=DC^2-AC^2=20^2-16^2=144\)
\(\Rightarrow AD=12\left(cm\right)\)
Bài 3:
Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC hay MN//PH
Do đó MNPH là hình thang
Xét tg AHC vuông tại H có HN là trung tuyến ứng vs ch AC nên \(HN=\dfrac{1}{2}AC\)
Mà P,M là trung điểm BC,AB nên PM là đtb tg ABC
Do đó \(PM=\dfrac{1}{2}AC\)
Từ đó ta được PM=HN
Vậy MNPH là hình thang cân

a, Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC
b, Vì MN là đtb tg ABC nên \(MN=\dfrac{1}{2}BC=6\left(cm\right)\)
c, Vì MN//BC nên BMNC là hình thang
Tự vẽ hình
Ta có: AM=BM(gt),AN=CN(gt)
=>MN là đường trung bình của tam giác ABC
=>\(MN=\frac{BC}{2}=\frac{10}{2}=5\left(cm\right)\)