Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Sửa đề: \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
Xét ΔAMN và ΔABC có
\(\widehat{AMN}=\widehat{ABC}\)(hai góc đồng vị, MN//BC)
\(\widehat{A}\) chung
Do đó: ΔAMN đồng dạng với ΔABC
=>\(\dfrac{AM}{AB}=\dfrac{MN}{BC}\)
b: \(\dfrac{MN}{BC}=\dfrac{AM}{AB}\)
=>\(\dfrac{MN}{8}=\dfrac{2}{5}\)
=>\(MN=2\cdot\dfrac{8}{5}=\dfrac{16}{5}\)

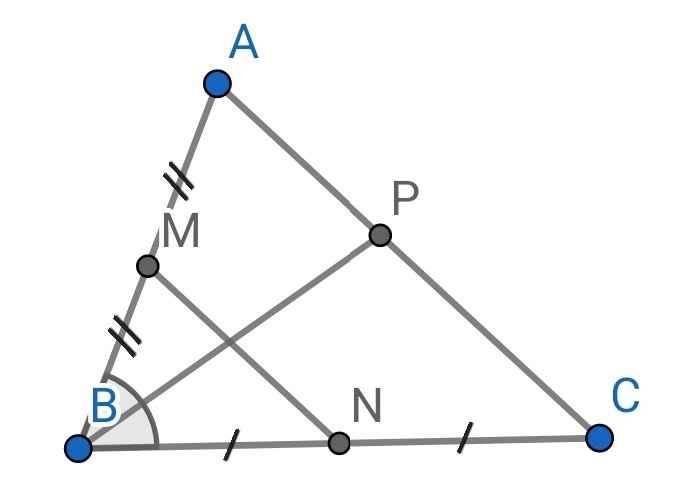 a) Do M là trung điểm của AB (gt)
a) Do M là trung điểm của AB (gt)
⇒ AM = BM = AB : 2 = 6 : 2 = 3 (cm)
Do N là trung điểm của BC (gt)
⇒ BN = CN = BC : 2 = 8 : 2 = 4 (cm)
Ta có:
BM/AM = 3/3 = 1
BN/CN = 4/4 = 1
⇒ BM/AM = BN/CN
⇒ MN // AC (định lý Ta-lét)
b) Ta có:
AM.BC = 3.8 = 24 (cm)
AB.BN = 6.4 = 24 (cm)
⇒ AM.BC = AB.BN
c) Do BP là tia phân giác của ∠ABC (gt)
⇒ BA/BC = PA/PC (1)
Do MN // AC (cmt)
⇒ BA/BC = AM/CN (2)
Từ (1) và (2) ⇒ AM/CN = PA/PC

a: AC=AB=15cm
MC=15-9=6cm
Xét ΔBACcó BM là phân giác
nên AM/AB=MC/BC
=>6/BC=9/15=3/5
=>BC=10cm
b: Xét ΔABM và ΔACN có
góc ABM=góc ACN
AB=AC
góc BAM chung
=>ΔABM=ΔACN
=>AM=AN
Xét ΔABC có AN/AB=AM/AC
nên MN//BC
c: Xét ΔABC cóMN//BC
nên AM/AC=MN/BC
=>MN/10=9/15=3/5
=>MN=6cm
Ta có : \(\dfrac{AM}{AB}=\dfrac{MN}{BC}\left(gt\right)\Rightarrow\)MN//BC