Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

(Mình chỉ giải câu c) theo yêu cầu thôi nhé ! :))
c) Ta có: AICK là hình bình hành (câu a)
Để AICK là hình thoi thì AC phải vuông góc với KI (2 đường chéo vuông góc với nhau)
mà KI // BC (BIKC là hình bình hành)
<=>AC vuông góc với BC
<=>tam giác ABC vuông tại C

a) Xét tứ giác AQMP có
PM//AQ(PM//AC, Q∈AC)
QM//AP(QM//AB, P∈AB)
Do đó: AQMP là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Bài 1:
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC
hay BMNC là hình thang
b: Xét ΔABK có MI//BK
nên MI/BK=AM/AB=1/2(1)
XétΔACK có NI//CK
nên NI/CK=AN/AC=1/2(2)
Từ (1)và (2) suy ra MI/BK=NI/CK
mà MI=NI
nên BK=CK
hay K là trug điểm của BC
Xét ΔABC có
K là trung điểm của BC
M là trung điểm của AB
Do đó: KM là đường trung bình
=>KM//AN và KM=AN
hay AMKN là hình bình hành

a: Xét ΔABC có
G là trung điểm của BC
F là trung điểm của AC
DO đó: FG là đường trung bình
=>FG//AE và FG=AE
=>AEGF là hình bình hành
mà \(\widehat{FAE}=90^0\)
nên AEGF là hình chữ nhật
b: Xét tứ giác BEIF có
IF//BE
EI//BF
Do đó: BEIF là hình bình hành
c: Ta có: EIFB là hình bình hành
nên FI//EB và FI=EB
=>FI=1/2IG
=>F là trung điểm của IG
Xét tứ giác CIAG có
F là trung điểm của AC
F la trung điểm của GI
Do đó: CIAG là hình bình hành
mà GA=GC
nên CIAG là hình thoi

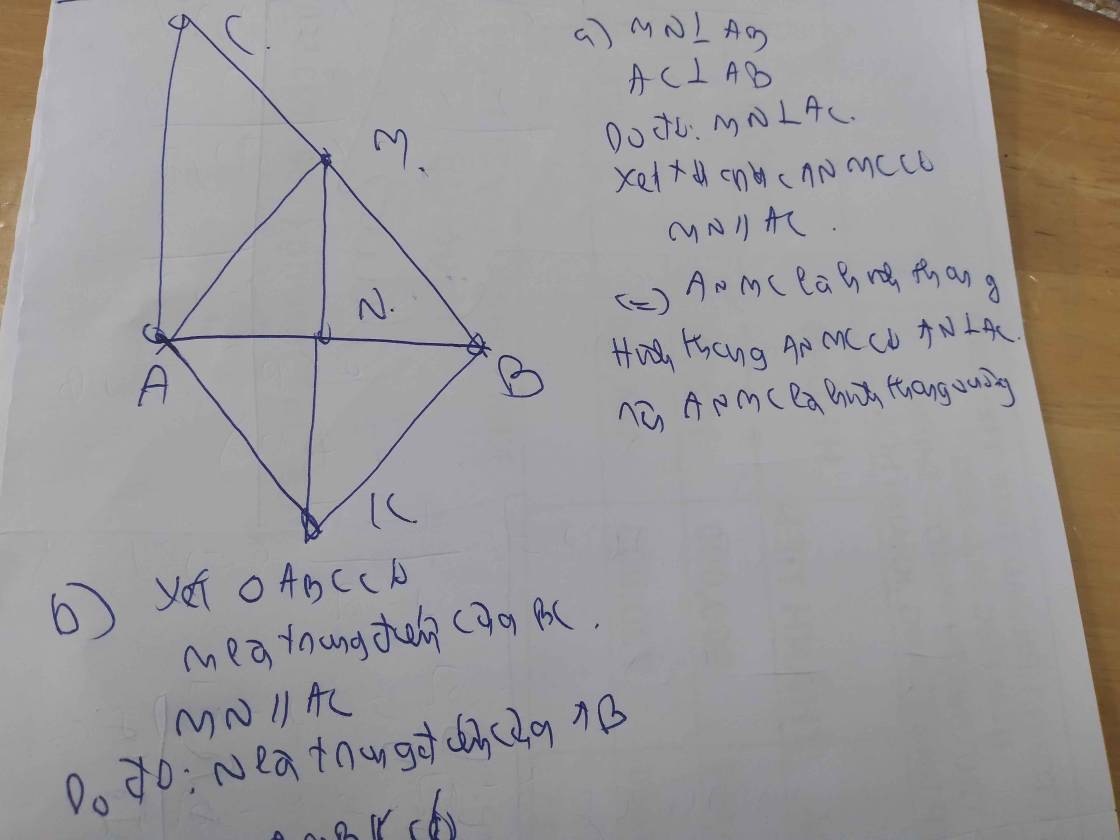
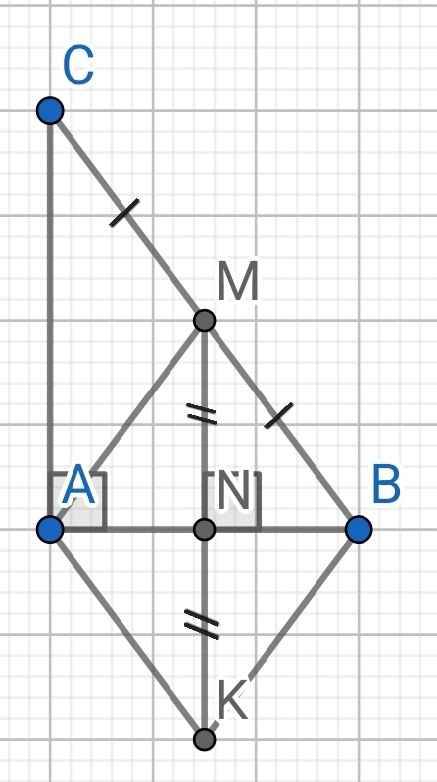 a) Do MN ⊥ AB (gt)
a) Do MN ⊥ AB (gt)
AC AB (do ∆ABC vuông tại A)
⇒ MN // AC
Tứ giác ANMC có:
MN // AC (cmt)
⇒ ANMC là hình thang
Mà ∠CAN = 90⁰
⇒ ANMC là hình thang vuông
b) ∆ABC có:
MN // AC (cmt)
M là trung điểm của BC
⇒ N là trung điểm của AB
Do MN ⊥ AB (gt)
⇒ MK ⊥ AB
Tứ giác AKBM có:
N là trung điểm của AB (cmt)
N là trung điểm của MK (gt)
⇒ AKBM là hình bình hành
Mà MK ⊥ AB (cmt)
⇒ AKBM là hình thoi
c) Để AKBM là hình vuông thì
AM ⊥ MB
⇒ AM ⊥ BC
⇒ AM là đường cao của ∆ABC
Mà AM là đường trung tuyến của ∆ABC (do M là trung điểm của BC)
⇒ ∆ABC có AM vừa là đường cao, vừa là đường trung tuyến
⇒ ∆ABC cân tại A
Mà ∆ABC vuông tại A (gt)
⇒ ∆ABC vuông cân tại A
Vậy để AKBM là hình vuông thì ∆ABC vuông cân tại A

a) ta có góc DMA=MAN=DAN=900
=> tứ giác AMDN là hình chữ nhật
b) ta có DB=DC VÀ DN // MA ( do MDNA là hình chữ nhật )
=> DN là đường trung bình của tam giác ABC
--> AN=NC hay N là trung điểm của AC
c) ta có tứ giác ADCE có 2 đường chéo cắt nhau tại trung điểm của mỗi đường nên là hình bình hành. Hình bình hành ADCE có 2 đường chéo vuông góc với nhau nên là hình thoi
d)

a)Xét tứ giác AMDN ,có:
góc MAN=90(ΔABC vuông tại A)
góc AMD=90(DM⊥AB)
góc AND=90(DN⊥AC)
⇒Tứ giác AMDN là hình vuông
b)Xét △ABC vuông tại A,có:
AD là đường trung tuyến ứng vs cạnh huyền BC
⇒AD=1/2 BC hay AD=DC
Xét △ADC có:
AD=DC(cmt)
⇒△ADC là tam giác cân tại D
Xét △ADC cân tại D,có:
AN là đường cao (DN⊥AC)
⇒N là trung điểm AC
c)Xét tứ giác ADCE,có:
N là trung điểm DE
N là trung điểm AC
mà DE và AC là 2 đg chéo cắt nhau tại N
⇒tứ giác ADCE là hình bình hành
Xét hbh ADCE ,có:
ND⊥AC
⇒hbh ADCE là hình thoi
Xét hình chữ nhật AMDN ,có:
DN=AN hay DN=AN=NE=NC hay DE=AC
Xét hình thoi ADCE có :
DE=AC
mà DE và AC là 2 đg chéo
⇒ADCE là hình vuông
d)Giả sử tứ giác ABCE là hình thang cân
⇔góc B=góc C
⇔△ABC là tam giác vuông cân tại A
Vậy để tứ giác ABCE là hình thang cân thì △ABC là tam giác vông cân tại A
a)Xét tứ giác AMDN ,có:
góc MAN=90(ΔABC vuông tại A)
góc AMD=90(DM⊥AB)
góc AND=90(DN⊥AC)
⇒Tứ giác AMDN là hình vuông
b)Xét △ABC vuông tại A,có:
AD là đường trung tuyến ứng vs cạnh huyền BC
⇒AD=1/2 BC hay AD=DC
Xét △ADC có:
AD=DC(cmt)
⇒△ADC là tam giác cân tại D
Xét △ADC cân tại D,có:
AN là đường cao (DN⊥AC)
⇒N là trung điểm AC
c)Xét tứ giác ADCE,có:
N là trung điểm DE
N là trung điểm AC
mà DE và AC là 2 đg chéo cắt nhau tại N
⇒tứ giác ADCE là hình bình hành
Xét hbh ADCE ,có:
ND⊥AC
⇒hbh ADCE là hình thoi
Xét hình chữ nhật AMDN ,có:
DN=AN hay DN=AN=NE=NC hay DE=AC
Xét hình thoi ADCE có :
DE=AC
mà DE và AC là 2 đg chéo
⇒ADCE là hình vuông
d)Giả sử tứ giác ABCE là hình thang cân
⇔góc B=góc C
⇔△ABC là tam giác vuông cân tại A
Vậy để tứ giác ABCE là hình thang cân thì △ABC là tam giác vông cân tại A


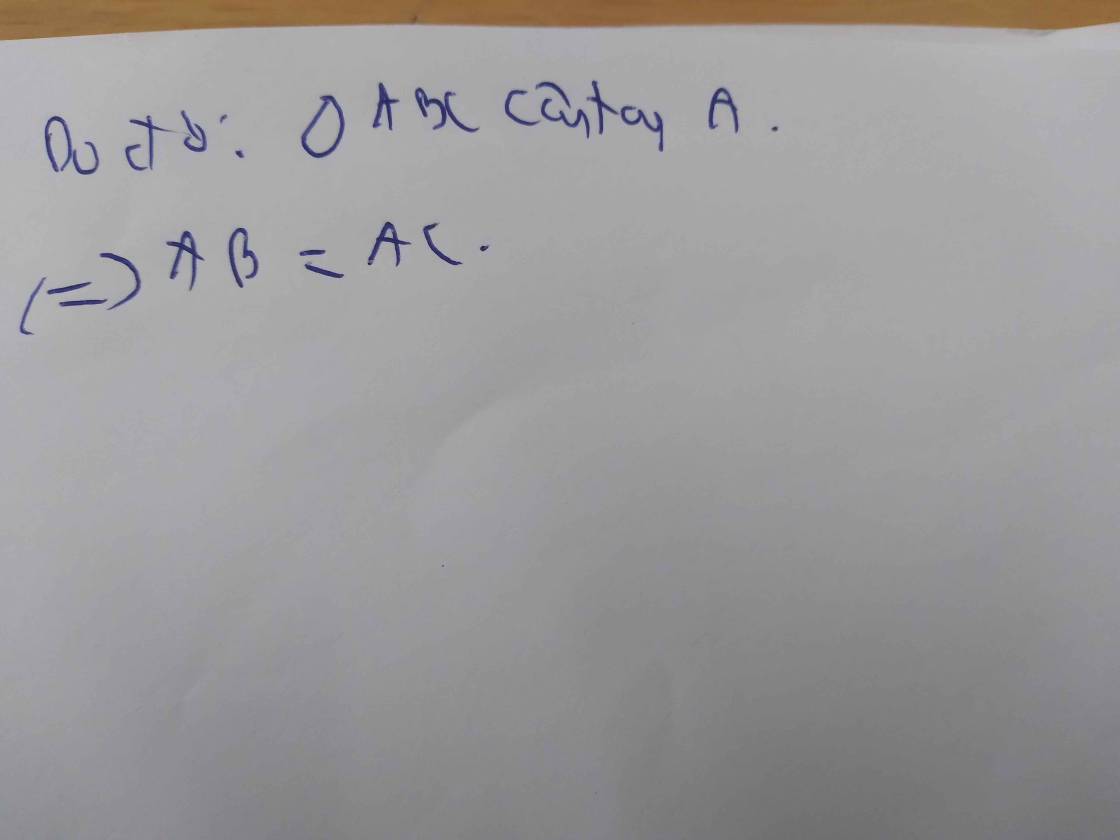
a: Xét tứ giác AIMK có
AI//MK
AK//MI
Do đó; AIMK là hình bình hành
b: để AIMK là hình chữ nhật thì góc A=90 độ