Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
Do đó: ΔABM=ΔACM

Không chắc lắm :v
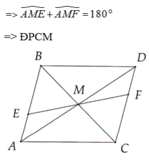
A B C M D
Dễ thấy AC = CD (do đoạn thẳngCA và CD có chung một hình chiếu và đường vuông góc AM = MD - Quan hệ giữa đường vuông góc và đường xiên,đường xiên và hình chiếu)
Xét \(\Delta MAB\) và \(\Delta MDC\) có:
AB = CD (vì AB = AC mà AC = CD)
BM = MC (gt)
AM = MD (gt)
Do đó \(\Delta MAB=\Delta MDC\) (c.c.c) (1)
Mà \(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh) (2)
Từ (1) và (2) suy ra AB // CD
À không nhầm mẹ rồi. Vẫn dùng cách hình hồi nãy nha! (không nhầm hoàn toàn,chỉ là nhầm một số chỗ,với lại không rõ ràng)
Dễ thấy AB = CD (Quan hệ đường vuông góc và đường xiên,đường xiên và hình chiếu) (1)
* Chứng minh \(\Delta MAB=\Delta MDC\)
Xét \(\Delta MAB\) và \(\Delta MDC\) có:
AB = CD - Từ (1)
MA = MD (gt)
MB = MC (gt)
Do đó \(\Delta MAB=\Delta MDC\) (c.c.c)
Suy ra \(\widehat{MAB}=\widehat{MDC}\) (hai góc tương ứng)
Mà hai góc này ở vị trí so le trong,do đó \(AB//CD^{\left(đpcm\right)}\)

\(a,\left\{{}\begin{matrix}AB=AC\\BM=MC\\AM\text{ chung}\end{matrix}\right.\Rightarrow\Delta AMB=\Delta AMC\left(c.c.c\right)\\ b,\left\{{}\begin{matrix}BM=MC\\\widehat{AMB}=\widehat{CMD}\left(đđ\right)\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMB=\Delta DMC\left(c.g.c\right)\\ \Rightarrow\widehat{ABC}=\widehat{BCD}\\ \text{Mà 2 góc này ở vị trí slt nên }AB\text{//}CD\\ c,\left\{{}\begin{matrix}BM=MC\\\widehat{AMC}=\widehat{BMD}\\AM=MD\end{matrix}\right.\Rightarrow\Delta AMC=\Delta DMB\left(c.g.c\right)\\ \Rightarrow\widehat{ACB}=\widehat{CBD}\\ \text{Mà 2 góc này ở vị trí slt nên }AC\text{//}BD\)

a: Xét ΔABM và ΔDCM có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC=BD
c: ABDC là hình bình hành
=>AB//DC

A B C M D
a) Xét \(\Delta ABMvà\Delta DCMcó:\)
MB=MC
góc AMB=góc CMD
MA=MD
\(\Rightarrow\Delta ABM=\Delta DCM\left(c-g-c\right)\)
b) Xét \(\Delta AMCvà\Delta BMDcó:\)
MC=MB
góc AMC=góc BMD
MA=MD
\(\Rightarrow\Delta AMC=\Delta DMB\left(c-g-c\right)\)
\(\Rightarrow AC=BD\)(cặp cạnh tương ứng)
c) Theo a), \(\Delta ABM=\Delta DCM\Rightarrow\)góc ABM=góc DCM (cặp góc tương ứng)
Mà 2 này tạo với BC hai góc so le trong nên AB//CD

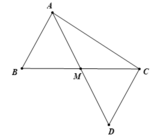
Xét \(\Delta ABM\) và \(\Delta DCM\) có
AM = DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh_
BM = CM (gt)
=> \(\Delta ABM\) = \(\Delta DCM\) (c.g.c)
=> AB = DC ( 2 cạnh t/ứ)
Xét \(\Delta ACM\) và \(\Delta DBM\) có
AM = DM (gt)
\(\widehat{AMC}=\widehat{BMD}\) (đối đỉnh)
CM = BM (gt)
=> \(\Delta ACM\) = \(\Delta DBM\) (c.g.c)
=> AC = DB ( 2 cạnh t/ứ)