Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AD}\)(D là trung điểm của BC) (1)
\(\overrightarrow{AM}+\overrightarrow{AN}=2\overrightarrow{AK}\)(K là trung điểm của MN) (2)
Lấy (1) trừ (2) có: \(\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=2\left(\overrightarrow{AD}-\overrightarrow{AK}\right)\)
⇔\(\dfrac{\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\overrightarrow{AM}+\overrightarrow{AN}\right)}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\left(\dfrac{1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\right)}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\overrightarrow{AB}+\overrightarrow{AC}-\dfrac{1}{2}\overrightarrow{AB}-\dfrac{1}{3}\overrightarrow{AC}}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{\dfrac{1}{2}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}}{2}\)=\(\overrightarrow{KD}\)
⇔\(\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)=\(\overrightarrow{KD}\)

\(\overrightarrow{KA}=-\overrightarrow{AK}=-\frac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=-\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right)\)
\(=-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\)
\(\overrightarrow{KD}=\overrightarrow{AD}-\overrightarrow{AK}=\overrightarrow{AD}+\overrightarrow{KA}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\)
\(=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\)

a)* NC= 2AN
NA+AC=2AN
AC=3AN
AN= 1/3 AC
*AK=1/2AN+ 1/2AM
AK= 1/2(1/3AC)+ 1/2(1/2AB)
AK=1/6AC+1/4AB
b)
KD=KA+AD
KD= -1/6AC-1/4AB+1/2AC+1/2AB
KD= 1/3AC+1/4AB
( tất cả đều là vecto)

chỗ Q là trung điểm của AN
suy ra MQ là đường trung bình sai r cô
A B C M N K I Q
\(\overrightarrow{BC}=\overrightarrow{BA}+\overrightarrow{AC}=\dfrac{1}{2}\overrightarrow{BM}+\dfrac{1}{3}\overrightarrow{NC}=\dfrac{1}{2}\left(\overrightarrow{BN}+\overrightarrow{NM}\right)+\)\(\dfrac{1}{3}\left(\overrightarrow{NM}+\overrightarrow{MC}\right)\)
\(=\dfrac{1}{2}\overrightarrow{BN}+\dfrac{1}{3}\overrightarrow{MC}+\dfrac{5}{6}\overrightarrow{NM}\).
Ta cần biểu diễn \(\overrightarrow{NM}\) theo hai véc tơ \(\overrightarrow{CM},\overrightarrow{BN}\).
Gọi I là giao điểm của CM và BN, Q là trung điểm của AN.
MQ là đường trung bình của tam giác ABN nên \(MQ=\dfrac{1}{2}BN\).
Do N là trung điểm của QC và IN // MQ nên I là trung điểm của MC.
Suy ra IN là đường trung bình của tam giác QMC và \(IN=\dfrac{1}{2}MQ\).
Mặt khác \(MQ=\dfrac{1}{2}BN\) nên \(MQ=\dfrac{1}{2}BN\).
Suy ra \(IN=\dfrac{1}{4}BN\).
Vì vậy \(\overrightarrow{NM}=\overrightarrow{NI}+\overrightarrow{IM}=-\dfrac{1}{4}\overrightarrow{BN}+\dfrac{1}{2}\overrightarrow{CM}\).
Từ đó ta có:
\(\overrightarrow{BC}=\dfrac{1}{2}\overrightarrow{BN}+\dfrac{1}{3}\overrightarrow{MC}+\dfrac{5}{6}\overrightarrow{NM}\)\(=\dfrac{1}{2}\overrightarrow{BN}+\dfrac{1}{3}\overrightarrow{MC}-\dfrac{1}{4}\overrightarrow{BN}+\dfrac{1}{2}\overrightarrow{CM}\)
\(=\dfrac{1}{2}\overrightarrow{BN}-\dfrac{1}{3}\overrightarrow{CM}-\dfrac{1}{4}\overrightarrow{BN}+\dfrac{1}{2}\overrightarrow{CM}\)
\(=\dfrac{1}{4}\overrightarrow{BN}+\dfrac{1}{6}\overrightarrow{CM}\).

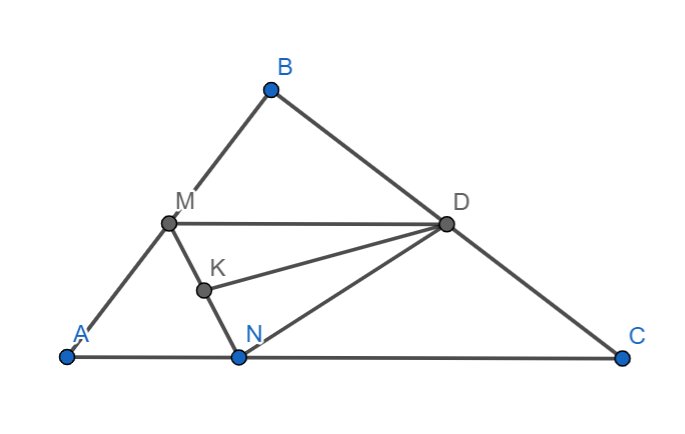
Xét \(\Delta ABC\) có:
\(M\) là trung điểm \(AB\)
\(D\) là trung điểm \(BC\)
\(\Rightarrow\) \(MD\) là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\) \(MD\)\(=\)\(\dfrac{1}{2}AC\) và \(MD\) //\(AC\)
Ta có:
\(\overrightarrow{KD}=\overrightarrow{KM}+\overrightarrow{MD}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NM}+\dfrac{1}{2}\overrightarrow{AC}\)
\(\Rightarrow\overrightarrow{KD}=\dfrac{1}{2}\overrightarrow{NA}+\dfrac{1}{2}\overrightarrow{AM}+\dfrac{1}{2}\overrightarrow{AC}=\dfrac{1}{6}\overrightarrow{CA}+\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{2}\overrightarrow{AC}\\ \Rightarrow\overrightarrow{KD}=\dfrac{1}{4}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
Có \(NC=2NA\Rightarrow\overrightarrow{NA}=\frac{1}{3}\overrightarrow{CA}\)
Có \(\overrightarrow{KD}=\overrightarrow{KM}+\overrightarrow{MB}+\overrightarrow{BD}\)
\(=\frac{1}{2}\overrightarrow{NM}+\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}\)
\(=\frac{1}{2}\left(\overrightarrow{NA}+\overrightarrow{AM}\right)+\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BA}+\frac{1}{2}\overrightarrow{AC}\)
\(=\frac{1}{2}\left(\frac{1}{3}\overrightarrow{CA}+\frac{1}{2}\overrightarrow{AB}\right)+\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BA}+\frac{1}{2}\overrightarrow{AC}\)
\(=\frac{1}{3}\overrightarrow{AC}+\frac{1}{4}\overrightarrow{AB}\)