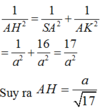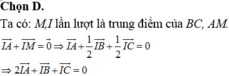
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

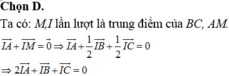

Đáp án là C.
• Gọi I là trung điểm của EC.
Ta có I M // B E hay I M // N E .
Xét Δ S M I có N E // M I và N là trung điểm của SM suy ra E là trung điểm của SI .
Do đó S E = E I = I C ⇒ S E S C = 1 3 .
Ta có V S A B E V S A B C = S A S A . S B S B . S E S C = 1 3
.

Đáp án C
Gọi H là trung điểm của AB. Do ∆ S A B đều nên S H ⊥ A B và S H = A B 3 2 = 2 3 .
Mà S A B ⊥ ( A B C D ) nên S H ⊥ ( A B C D ) .

Từ d S , A B C D d M , A B C D = S D M D = 2 ⇒ d M ; ( A B C D ) = d S ; A B C D 2 = S H 2 = 3 .
Ta có S ∆ P C N = 1 2 P C . P N = 1 2 . B C 2 . C D 2 = 1 2 . 4 2 . 4 2 = 2 (đvdt).
→ V M . P C N = 1 3 . d M ; ( A B C D ) . S ∆ P C N = 1 3 . 3 . 2 = 2 3 3 (đvdt) .
→ y = 2 3 3
Lại có S A B P N = S A B C D - S ∆ P C N = 4 2 - 1 2 . 2 . 2 - 1 2 . 4 . 2 = 10 (đvdt)
V S . A B P N = 1 3 . S H . S A B P N = 1 3 . 2 3 . 10 = 20 3 3 (đvdt) .
* Phương án A:
x 2 + 2 x y - y 2 = 20 3 3 2 + 2 . 20 3 3 . 20 3 3 - 2 3 3 2 = 476 3 < 160
* Phương án B:
x 2 - 2 x y + 2 y 2 = 20 3 3 2 - 2 . 20 3 3 . 20 3 3 + 2 2 3 3 2 = 328 3 > 109
* Phương án C:
x 2 + x y - y 4 = 20 3 3 2 + 20 3 3 . 20 3 3 - 2 3 3 4 = 1304 9 < 145
* Phương án D:
x 2 - x y + y 4 = 20 3 3 2 - 20 3 3 . 20 3 3 + 2 3 3 4 = 1096 9 < 125


Chọn B.
Gọi E là trung điểm của MC. Qua A kẻ một đường thẳng song song với BC cắt đường thẳng NE tại K.
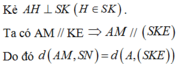
Ta dễ chứng minh được A H ⊥ S K E nên d A ; S K E = A H . Tam giác SAKvuông ở A và có AH là đường cao nên