Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H N M 3 4
Xét \(\Delta HAC\)vuông tại H có HN là đường trung tuyến ứng với cạnh huyền
=> HN = NC = NA = AC/2
=> AC = 2HN = 8
Tương tự AB = 6
Theo hệ thức lượng trong tam giác vuông cho tam giác ABC vuông tại A có AH là đường cao thì
\(\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{1}{6^2}+\frac{1}{8^2}\)
\(\Leftrightarrow\frac{1}{AH^2}=\frac{25}{576}\)
\(\Leftrightarrow AH=\frac{24}{5}\)
Áp dụng định lí Pytago vào \(\Delta HAC\)vuông tại H có
\(HA^2+HC^2=AC^2\)
\(\Leftrightarrow\left(\frac{24}{5}\right)^2+HC^2=8^2\)
\(\Leftrightarrow HC=\frac{32}{5}\)
Tương tự \(HB=\frac{18}{5}\)

Gọi I là giao điểm của đường trung trực đoạn HC và tia phân giác ^BHC => I là điểm cố định
I nằm trên đường trung trực của HC nên IH = IC => ∆IHC cân tại I => ^IHC = ^ICH
Lại có: ^IHC = ^IHM (Do HI là tia phân giác của ^BHC, theo cách chọn điểm phụ) => ^IHM = ^ICH hay ^IHM = ^ICN
Xét ∆ICN và ∆IHM có:
IC = IH (theo cách chọn hình phụ)
^ICN = ^IHM (cmt)
CN = HM (gt)
Do đó ∆ICN = ∆IHM (c.g.c)
=> IN = IM (hai cạnh tương ứng)
Do đó I thuộc đường trung trực của MN
Vậy đường trung trực của MN luôn đi qua một điểm cố định I (đpcm)


Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{7}\)
nên \(\dfrac{HB}{HC}=\dfrac{9}{49}\)
hay \(HB=\dfrac{9}{49}HC\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC^2\cdot\dfrac{9}{49}=42^2\)
hay HC=98cm
\(\Leftrightarrow HB=\dfrac{9}{49}\cdot98=18cm\)
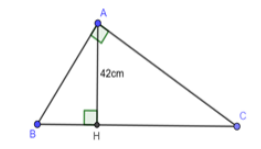
Ta có:\(\dfrac{AB}{AC}=\dfrac{3}{7}\) ⇒ AB = \(\dfrac{3}{7}\) AC
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{42^2}=\dfrac{49}{9AC^2}+\dfrac{1}{AC^2}\Leftrightarrow\dfrac{1}{42^2}=\dfrac{49}{9AC^2}\)
⇔ \(AC^2=11368\Leftrightarrow AC=14\sqrt{58}\) \(\left(cm\right)\)
⇔ \(AB=\dfrac{3}{7}.14\sqrt{58}=6\sqrt{58}\) \(\left(cm\right)\)
Áp dụng định lý Pytago cho ABH vuông tại A có: \(AB^2+AC^2=BC^2\)
⇔ \(BC^2=\left(6\sqrt{58}\right)^2+\left(14\sqrt{58}\right)^2\)
⇔ \(BC^2=13456\Rightarrow BC=116\) \(cm\)
Áp dụng hệ thức lượng trong ABC vuông tại A có đường cao AH ta có:

b: \(AN\cdot AC=AH^2\)
\(AC^2-HC^2=AH^2\)
Do đó: \(AN\cdot AC=AC^2-HC^2\)

a: BC=căn 15^2+20^2=25cm
AH=15*20/25=12cm
HB=15^2/25=9cm
HC=25-9=16cm
AD là phân giác
=>BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=25/7
=>BD=75/7cm; CD=100/7cm
b: ΔAHB vuông tại H có HI là đường cao
nên AI*AB=AH^2
ΔAHC vuông tại H có HK là đường cao
nên AK*AC=AH^2
=>AI*AB=AK*AC
c: AI*AB=AK*AC
=>AI/AC=AK/AB
=>ΔAIK đồng dạng với ΔACB
sai đề bài rồi tuấn sao lại 2 cái HC
BÀI NÀY NẾU CHỈ NÓI ĐỒNG QUY THÌ NHIỀU TRƯỜNG HỢP LẮM NÀO THÌ GIAO 3 ĐƯỜNG TRUNG TUYẾN; PHÂN GIÁC;ĐƯỜNG CAO