Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có \(\overrightarrow{v}=\overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{CM}\)
\(=\left(\overrightarrow{CM}+\overrightarrow{MA}\right)+\left(\overrightarrow{CM}+\overrightarrow{MB}\right)=\overrightarrow{CA}+\overrightarrow{CB}\) (Không phụ thuộc vào vị trí điểm M).
A B C I K
b) Dựng hình bình hành BCAD. Theo quy tắc hình bình hành:
\(\overrightarrow{CA}+\overrightarrow{CB}=\overrightarrow{CD}\).
Vậy \(\overrightarrow{CD}=\overrightarrow{v}\).
\(\overrightarrow{v}=\overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC}\)
\(=2\overrightarrow{ME}-2\overrightarrow{MC}\) (E là trung điểm cạnh AB)
\(=\left(\overrightarrow{ME}-MC\right)=2\overrightarrow{CE}\)
vậy \(\overrightarrow{v}\) không phụ thuộc vị trí của điểm M
\(\overrightarrow{CD}=\overrightarrow{v}=2\overrightarrow{CE}\) thì E là trung điểm của CD
\(\Rightarrow\) ta dựng được điểm D

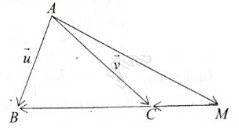
Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)

A B C D I K
a)
- \(\overrightarrow{BI}=\frac{1}{2}\left(\overrightarrow{BA}+\overrightarrow{BD}\right)\) (t/c trung điểm)
\(=\frac{1}{2}\left(\overrightarrow{BA}+\frac{1}{2}\overrightarrow{BC}\right)\)
\(=\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\)
- \(\overrightarrow{BK}=\overrightarrow{BA}+\overrightarrow{AK}\)
\(=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{AC}\)
\(=\overrightarrow{BA}+\frac{1}{3}\left(\overrightarrow{BC}-\overrightarrow{BA}\right)\)
\(=\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}-\frac{1}{3}\overrightarrow{BA}\)
\(=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}\)
b) Ta có: \(\overrightarrow{BK}=\frac{2}{3}\overrightarrow{BA}+\frac{1}{3}\overrightarrow{BC}=\frac{4}{3}\left(\frac{1}{2}\overrightarrow{BA}+\frac{1}{4}\overrightarrow{BC}\right)=\frac{4}{3}\overrightarrow{BI}\)
=> B,K,I thẳng hàng
c) \(27\overrightarrow{MA}-8\overrightarrow{MB}=2015\overrightarrow{MC}\)
\(\Leftrightarrow27\left(\overrightarrow{MC}+\overrightarrow{CA}\right)-8\left(\overrightarrow{MC}+\overrightarrow{CB}\right)=2015\overrightarrow{MC}\)
\(\Leftrightarrow27\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{MC}-8\overrightarrow{CB}-2015\overrightarrow{MC}=\overrightarrow{0}\)
\(\Leftrightarrow-1996\overrightarrow{MC}+27\overrightarrow{CA}-8\overrightarrow{CB}=\overrightarrow{0}\)
\(\Leftrightarrow1996\overrightarrow{CM}=8\overrightarrow{CB}-27\overrightarrow{CA}\)
\(\Leftrightarrow\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}\)
Vậy: Dựng điểm M sao cho \(\overrightarrow{CM}=\frac{8\overrightarrow{CB}-27\overrightarrow{CA}}{1996}\)

Ta có:
\(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{MB}+4\overrightarrow{MC}\)
\(=6\overrightarrow{MI}+\overrightarrow{IA}+\overrightarrow{IB}+4\overrightarrow{IC}\)
\(=6\overrightarrow{MI}+4\overrightarrow{IG}+4\overrightarrow{IC}\)
\(=6\overrightarrow{MI}\)
\(\Rightarrow M,I,N\) thẳng hàng
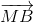 = 3
= 3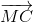 =>
=> 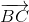 )
)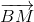 =
= 
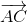 -
- 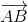 nên
nên 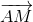 =
= 