Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.trong tam giác ADK :
AB=BD (D đối xứng vs A qua B)
N là trung điểm của AK
=>BN là đg trung bình của tam giác ADK
=> BN//DK
=>BN//MK
trong tam giác NBC có:
BN//MK
M là trung điểm của BC
=>NK=KC
mà NK=AN
=>AN=NK=KC
=>2NA=NC

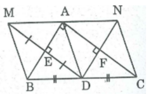
Tứ giác ADBM là hình thoi ⇒ AM // DB và AM = AD
Hay AM // BC và AM = AD (1)
Tứ giác ADCN là hình thoi ⇒ AN // DC và AD = AN
Hay AN // BC và AN = AD (2)
Từ (1) và (2) suy ra: AM trùng với AN hay M, A, N thẳng hàng
Và AM = AN nên A là trung điểm của MN
Vậy điểm M và điểm N đối xứng qua điểm A.

a: M đối xứng A qua BC
nên BC là trung trực của AM
=>BA=BM; CA=CM
mà BA=CA
nên BA=BM=CA=CM
=>ABMC là hình thoi
b: Xét tứ giác AHCI có
K là trung điểm chung của AC và HI
góc AHC=90 độ
Do đó: AHCI là hình chữ nhật
c: Xét ΔBAC có CH/CB=CK/CA
nen HK//AB và HK=AB/2
=>HK//AD và HK=AD
=>ADHK là hình bình hành
=>AH cắt DK tại trung điểm của mỗi đường(1)
Xét tứ giác AIHB có
AI//HB
AI=HB
Do đó: AIHB là hình bình hành
=>AH cắt IB tại trung điểm của mỗi đường(2)
Từ (1), (2) suy ra AH,IB,DK đồng quy

A B C D M K H
Từ B kẻ BH // AC
Ta có: AB = BD, BH // AC
=> BH là đường trung bình của \(\Delta ADK\)
=> \(BH=\dfrac{1}{2}AK\) (tính chất đường trung bình của tam giác)
Xét \(\Delta BHM\) và \(\Delta CKM\) có:
\(\widehat{KMC}=\widehat{BHM}\) (2 góc đối đỉnh)
CM = MB (M trung điểm CB)
\(\widehat{MBH}=\widehat{CKM}\) (KC // BH)
=> \(\Delta BHM=\Delta CKM\left(g.c.g\right)\)
=> KC = BH (2 cạnh tương ứng)
mà \(BH=\dfrac{1}{2}AK\) (cmt)
=> \(KC=\dfrac{1}{2}AK\)
\(\Rightarrow AK=2KC\left(đpcm\right)\)
A B K C H M D
Từ B kẻ BH // AC
Ta có: AB = BD, BH // AC
=> BH là đường trung bình của \(\Delta ADK\)
=>BH=\(\dfrac{1}{2}AK\)(tính chất đường trung bình của tam giác)
Xét \(\Delta BHM\)và \(\Delta CKM\) có :
\(\widehat{KMC}=\widehat{BMH}\) ( hai góc đối đỉnh )
CM=MB (M la ftrung điểm của CB)
\(\widehat{MBH}=\widehat{CKM}\) ( KC//BH )
=>\(\widehat{BHM}=\widehat{CKM}\)
=>KC = BH
mà BH=1/2 AK
=>\(KC=\dfrac{1}{2}AK\)
=>AK=2KC
=> đcpm