Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử tứ giác ABCD định hướng âm. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{3}\) ta có
\(\overrightarrow{EG}=\overrightarrow{AG}-\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BG}-\overrightarrow{AE}\)
suy ra \(f\left(\overrightarrow{EG}\right)=f\left(\overrightarrow{AB}\right)+f\left(\overrightarrow{BG}\right)-f\left(\overrightarrow{AE}\right)\)
\(=\overrightarrow{AE}+\overrightarrow{BC}-\overrightarrow{BE}\)
\(=\overrightarrow{AC}\)
Tương tự ta cũng chứng minh được \(f\left(\overrightarrow{HF}\right)=\overrightarrow{AC}\)
Từ đó suy ra \(\overrightarrow{EG}=\overrightarrow{HF}\)
Do đó tứ giác EGFH là hình bình hành

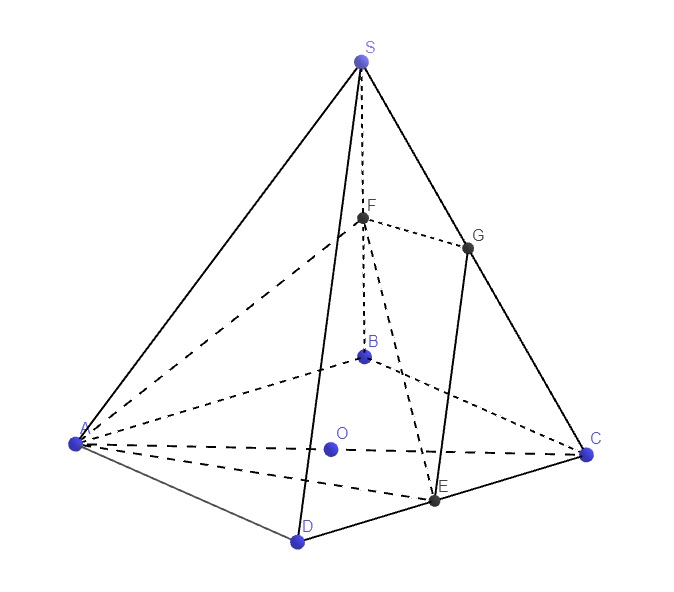
Qua E kẻ đường thẳng song song SD cắt SC tại G \(\Rightarrow\dfrac{GC}{GS}=\dfrac{EC}{ED}\) (Talet)
Mặt khác theo định lý phân giác: \(\dfrac{EC}{ED}=\dfrac{AC}{AD}\Rightarrow\dfrac{GC}{GS}=\dfrac{AC}{AD}=\dfrac{AB}{SA}\) (do AC=AB và AD=SA)
Theo định lý phân giác: \(\dfrac{AB}{SA}=\dfrac{FB}{FS}\Rightarrow\dfrac{GC}{GS}=\dfrac{FB}{FS}\Rightarrow FG||BC\Rightarrow FG||AD\)
\(\Rightarrow\left(EFG\right)||\left(SAD\right)\Rightarrow EF||SAD\)

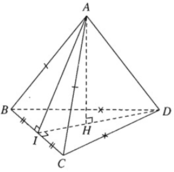
a) Tam giác ABC cân đỉnh A và có I là trung điểm của BC nên AI ⊥ BC. Tương tự tam giác DBC cân đỉnh D và có có I là trung điểm của BC nên DI ⊥ BC. Ta suy ra:
BC ⊥ (AID) nên BC ⊥ AD.
b) Vì BC ⊥ (AID) nên BC ⊥ AH
Mặt khác AH ⊥ ID nên ta suy ra AH vuông góc với mặt phẳng (BCD).

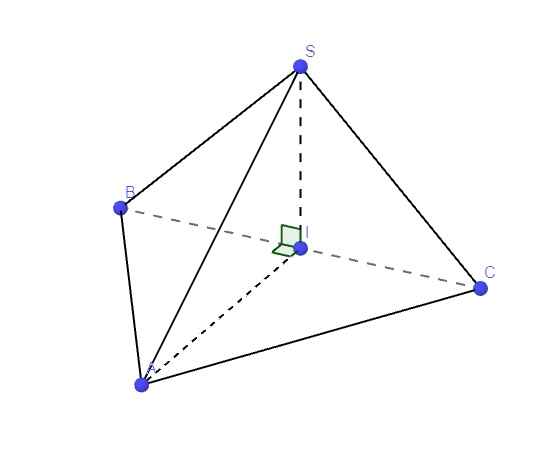
a.
Do ABC đều \(\Rightarrow\) AI là trung tuyến đồng thời là đường cao
\(\Rightarrow AI\perp BC\) (1)
SBC vuông cân tại S \(\Rightarrow SI\) là trung tuyến kiêm đường cao
\(\Rightarrow SI\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAI\right)\Rightarrow BC\perp SA\)
b.
\(SA>AI\Rightarrow\widehat{SIA}>\widehat{ASI}\Rightarrow\widehat{ASI}\) là góc nhọn
Do ABC đều \(\Rightarrow AI=\dfrac{a\sqrt{3}}{2}\)
SBC vuông cân tại S \(\Rightarrow SI=\dfrac{1}{2}BC=\dfrac{a}{2}\)
Áp dụng định lý hàm sin cho tam giác SAI:
\(\dfrac{SI}{sin\widehat{IAS}}=\dfrac{AI}{sin\widehat{ASI}}\Rightarrow sin\widehat{ASI}=\dfrac{\sqrt{3}}{2}\)
\(\Rightarrow\widehat{ASI}=60^0\) (do \(\widehat{ASI}\) nhọn)
\(\Rightarrow=180^0-\left(30^0+60^0\right)=90^0\)
Hay \(SI\perp IA\)

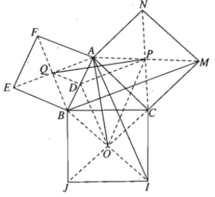
a) Phép quay tâm C góc 90 ο biến MB thành AI. Do đó MB bằng và vuông góc với AI. DP song song và bằng nửa BM, DO song song và bằng nửa AI. Từ đó suy ra DP bằng và vuông góc với DO.
b) Từ câu a) suy ra phép quay tâm D, góc 90 ο biến O thành P, biến A thành Q. Do đó OA bằng và vuông góc với PQ.
Gọi D, E và F theo thứ tự là trung điểm các cạnh BC, CA và AB của tam giác ABC. Ta có :
\(\overrightarrow{AB'}=\overrightarrow{AE}+\overrightarrow{EB'}=\frac{1}{2}\overrightarrow{c}+\overrightarrow{EB'}\)
\(\overrightarrow{AC'}=\overrightarrow{AF}+\overrightarrow{FC'}=\frac{1}{2}\overrightarrow{b}+\overrightarrow{FC'}\)
\(\overrightarrow{AA'}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{DA'}=\frac{1}{2}\overrightarrow{b}+\frac{1}{2}\overrightarrow{c}+\overrightarrow{DA}\)
Do đó, điều phải chứng minh tương đương với
\(\overrightarrow{AB'}=\overrightarrow{FC'}=\overrightarrow{DA'}\)
Giả sử tam giác ABC định hướng dương. Gọi \(f\) là phép quay vec tơ theo góc \(\frac{\pi}{2}\) và
\(k=\cot\widehat{B'AC}=\cot\widehat{C'AB}\)
Ta có
\(f\left(\overrightarrow{EB'}+\overrightarrow{FC'}\right)=f\left(\overrightarrow{EB'}\right)+f\left(\overrightarrow{FC'}\right)\)
\(=k\overrightarrow{EA}+k\overrightarrow{AF}=\frac{k}{2}\left(\overrightarrow{b}-\overrightarrow{c}\right)\) (do \(\overrightarrow{CA}+\overrightarrow{AB}+\overrightarrow{BC}=0\) )
\(=\frac{k}{2}\overrightarrow{CB}=k\overrightarrow{DB}=f\left(\overrightarrow{DA'}\right)\)
Suy ra điều cần chứng minh
A B C C' B' A' E F D b c