Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

xét tam giác ABC có góc A+B+C=180
100+50+C=180
C=180-100-50=30
xét tam giác ABI và Dci
IA=ID (gt)
IB=IC (gt)
AIB=CID (đ.đỉnh)
Vậy tam giác ABI=DCI (c.g.c)
Vậy góc ABI=DCI (2gocs tưng ứng)
Xét tam giác MIB và NIC
B =ICD (cmt)
IB=IC (gt)
MIB=NIC (đ.đỉnh)
Vậy tan giác MIB=NIC (g.c.g)
vậy IM=IN (2 cạnh tương ứng)
vậy I là trung điểm của MN
xét tam giác ABC có góc A+B+C=180
100+50+C=180
C=180-100-50=30
xét tam giác ABI và Dci
IA=ID (gt)
IB=IC (gt)
AIB=CID (đ.đỉnh)
Vậy tam giác ABI=DCI (c.g.c)
Vậy góc ABI=DCI (2gocs tưng ứng)
Xét tam giác MIB và NIC
B =ICD (cmt)
IB=IC (gt)
MIB=NIC (đ.đỉnh)
Vậy tan giác MIB=NIC (g.c.g)
vậy IM=IN (2 cạnh tương ứng)
vậy I là trung điểm của MN

a: Xét ΔABI vuông tại I và ΔACI vuông tại I có
AI chung
BI=CI
Do đó: ΔABI=ΔACI
b: Ta có: ΔABI=ΔACI
nên AB=AC
hay ΔABC cân tại A
c: Xét tứ giác ABDC có
I là trung điểm của BC
I là trung điểm của AD
Do đó:ABDC là hình bình hành
Suy ra: AB//CD

B D I A C 1 2 1 2
a) *Xét ΔABI và ΔDCI có:
\(\left\{{}\begin{matrix}BI=CI\left(gt\right)\\\widehat{I_1}=\widehat{I_2}\left(\text{đ}\text{ối}.\text{đ}\text{ỉnh}\right)\\AI=ID\left(gt\right)\end{matrix}\right.\)
⇒ ΔABI = ΔDCI (c - g - c)
b) *Vì ΔABI = ΔDCI (cmt)
⇒ AB = CD (hai cạnh tương ứng) ⇒ \(\widehat{A}_1=\widehat{D}\) (hai góc tương ứng) Mà \(\widehat{A_1}\) và \(\widehat{D}\) nằm ở vị trí so le trong ⇒ AB // CD
\(\text{a)}\text{Xét }\Delta ABI\text{ và }\Delta ACI\text{ có:}\)
\(AB=AC\left(gt\right)\)
\(BI=CI\text{(I trung điểm BC)}\)
\(AI\text{ chung}\)
\(\Rightarrow\Delta ABI=\Delta ACI\left(c.c.c\right)\)
\(\text{b)Xét }\Delta AIC\text{ và }\Delta DIB\text{ có:}\)
\(AI=DI\left(gt\right)\)
\(\widehat{AIC}=\widehat{DIB}\text{(đối đỉnh)}\)
\(IC=IB\)
\(\Rightarrow\Delta AIC=\Delta DIB\left(c.g.c\right)\)
\(\Rightarrow\widehat{DIB}=\widehat{ICA}\text{(2 góc tương ứng)}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow AC=BD\)
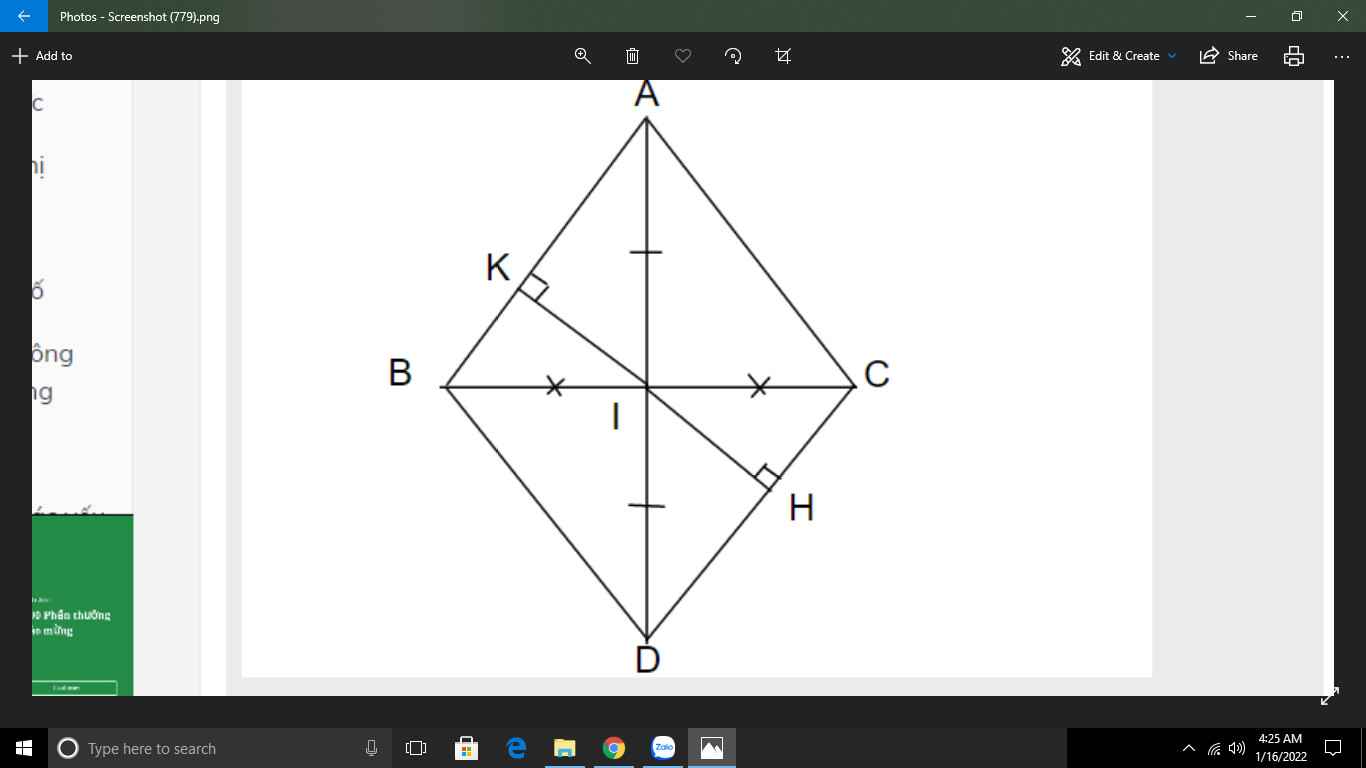
\(\text{c)Xét }\Delta IKB\text{ và }\Delta IHC\text{ có:}\)
\(\widehat{IKB}=\widehat{IHC}=90^0\)
\(IB=IC\)
\(\widehat{KIB}=\widehat{CIH}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta IKB=\Delta IHC\left(ch-gn\right)\)
\(\Rightarrow IK=IH\)
\(\text{Hình có chỗ nào bạn ko thấy rõ thì ib riêng cho mik nghe:3}\)

a: góc C=180-100-50=30 độ
b: Xét ΔABI và ΔDCI có
IA=ID
góc AIB=góc DIC
IB=IC
Do đó: ΔABI=ΔDCI
c: Xét ΔICN vuông tại N và ΔIBM vuông tại M có
IC=IB
góc ICN=góc IBM
Do đó: ΔICN=ΔIBM
=>góc CIN=góc BIM và IM=IN
=>góc CIN+góc CIM=180 độ
=>M,I,N thẳng hàng và IM=IN
=>I là trung điểm của MN