Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) I là trung điểm
nên vectoAB+ vectoAC= 2AI (1)
vectoAD+ vectoAE=2AI (2)
Từ (1) và (2) suy ra câu a
b) vecto AB+ vectoAC= 2AI(cmt
vectoAD+ vectoAE= 2AI(cmt
vectoAS=vectoAB+ vectoAD+ vectoAC+ vectoAE
tương đương: vectoAS=(vectoAB+ vectoAC)+ (vectoAD+ vectoAE)
vectoAS=2AI+2AI= 4AI

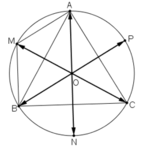
a) 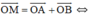 M là đỉnh còn lại của hình bình hành AOBM.
M là đỉnh còn lại của hình bình hành AOBM.
+ AOBM là hình bình hành ⇒ AM = OB
Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1)
+ AOBM là hình bình hành ⇒ AM//BO
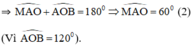
Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC.
Mà 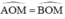 nên M là điểm chính giữa cung
nên M là điểm chính giữa cung 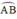
b) Chứng minh tương tự phần a) ta có: 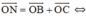 N là điểm chính giữa cung BC.
N là điểm chính giữa cung BC.
c) 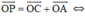 P là điểm chính giữa cung CA.
P là điểm chính giữa cung CA.

A B C B'
Dựng điểm B' sao cho C là trung điểm BB', suy ra \(\overrightarrow{BC}=\overrightarrow{CB'}\).
\(\left(\overrightarrow{CA},\overrightarrow{BC}\right)=\left(\overrightarrow{CA},\overrightarrow{CB'}\right)=\widehat{ACB'}\).
\(BC^2=\sqrt{AB^2+AC^2}=5\).
\(cos\widehat{BCA}=\dfrac{3}{5}\).
\(cos\left(\overrightarrow{CA},\overrightarrow{BC}\right)=cos\left(\overrightarrow{CA},\overrightarrow{CB'}\right)=cos\widehat{ACB'}=-\dfrac{3}{5}\).

+) vecto AC + vecto BD = vecto AD + vecto DC + vecto BC + vecto CD
= vecto AD + vecto BC (1)
+) vecto MN = \(\frac{1}{2}\left(\overrightarrow{MD}+\overrightarrow{MC}\right)\)
\(\Leftrightarrow2\overrightarrow{MN}=\overrightarrow{MD}+\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{AD}+\overrightarrow{MB}+\overrightarrow{BC} \)\(=\overrightarrow{AD}+\overrightarrow{BC}\)\(\left(2\right)\)
Từ (1),(2) => đpcm

1) Có \(2\overrightarrow{EF}=\overrightarrow{ED}+\overrightarrow{EC}\)
Lại có : \(\left\{{}\begin{matrix}\overrightarrow{AD}=\overrightarrow{AE}+\overrightarrow{ED}\\\overrightarrow{BC}=\overrightarrow{BE}+\overrightarrow{EC}\end{matrix}\right.\rightarrow\overrightarrow{AD}+\overrightarrow{BC}=\left(\overrightarrow{AE}+\overrightarrow{BE}\right)+\overrightarrow{ED}+\overrightarrow{EC}=\overrightarrow{0}+\overrightarrow{ED}+\overrightarrow{EC}=\overrightarrow{ED}+\overrightarrow{EC}\) Do đó : \(2\overrightarrow{EF}=\overrightarrow{AD}+\overrightarrow{BC}\left(=\overrightarrow{ED}+\overrightarrow{EC}\right)\)
2) Có : \(\left\{{}\begin{matrix}\overrightarrow{OA}+\overrightarrow{OB}=2\overrightarrow{OE}\left(1\right)\\\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OF}=-2\overrightarrow{OE}\left(2\right)\end{matrix}\right.\)
(1) + (2) => \(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=2\overrightarrow{OE}+2\overrightarrow{OF}=2\overrightarrow{OE}-2\overrightarrow{OE}=\overrightarrow{0}\)
3) \(\left(\overrightarrow{AB}+\overrightarrow{AD}\right)+\overrightarrow{AC}=2\overrightarrow{AC}=4\overrightarrow{AO}\)
4) Ta có : \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}+\overrightarrow{MD}=\left(\overrightarrow{MO}+\overrightarrow{OA}\right)+\left(\overrightarrow{MO}+\overrightarrow{OB}\right)+\left(\overrightarrow{MO}+\overrightarrow{OC}\right)+\left(\overrightarrow{MO}+\overrightarrow{OD}\right)=4\overrightarrow{MO}+\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}\right)=4\overrightarrow{MO}+\overrightarrow{0}=4\overrightarrow{MO}\)

a: vecto AB-vecto AD
=vecto DA+vecto AB
=vecto DB
-vecto CD-veco BC
=vecto CB-vecto CD
=vecto DC+vecto CB=vecto DB
=>vecto AB+vecto CD=vecto AD-vecto BC
b: \(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CA}+\overrightarrow{AB}=\overrightarrow{CB}\)
\(\overrightarrow{CD}-\overrightarrow{BD}=\overrightarrow{CD}+\overrightarrow{DB}=\overrightarrow{CB}\)
Do đó: \(\overrightarrow{AB}-\overrightarrow{AC}=\overrightarrow{CD}-\overrightarrow{BD}\)
=>\(\overrightarrow{AB}-\overrightarrow{CD}=\overrightarrow{AC}-\overrightarrow{BD}\)
c: \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{DA}+\overrightarrow{AB}=\overrightarrow{DB}\)
\(\overrightarrow{CB}-\overrightarrow{CD}=\overrightarrow{DC}+\overrightarrow{CB}=\overrightarrow{DB}\)
Do đó: \(\overrightarrow{AB}-\overrightarrow{AD}=\overrightarrow{CB}-\overrightarrow{CD}\)
=>\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AD}+\overrightarrow{CB}\)

b) Dựng hình bình hành ABCD
Tam giác ABC đều:
Kẻ BH⊥AC ⇒BD⊥AC
Tam giác HAB vuông tại H:
BH=AB.sinA=a.sin60=\(\dfrac{a\sqrt{3}}{2}\)
BD=2AH=\(2.\dfrac{a\sqrt{3}}{2}=a\sqrt{3}\)
Vecto v=vectoBA+vectoBC=vectoBD
|vecto v|=|vectoBD|=BD=\(a\sqrt{3}\)
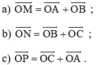


\(\overrightarrow{AD}=\overrightarrow{BC}\) \(\Rightarrow\) ABCD là hình bình hành
Vậy D là đỉnh của hình bình hành ABCD
\(\overrightarrow{AE}=\overrightarrow{CA}\Rightarrow\overrightarrow{AE}-\overrightarrow{CA}=\overrightarrow{0}\Rightarrow\overrightarrow{AE}+\overrightarrow{AC}=\overrightarrow{0}\)
\(\Rightarrow A\) là trung điểm CE hay E là điểm đối xứng C qua A