Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
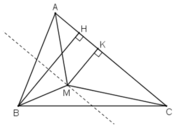
Kẻ đường cao BH, MK.
Ta có: SAMB + SBMC + SMAC = SABC (1)
Mà SAMB + SBMC = SMAC (2)
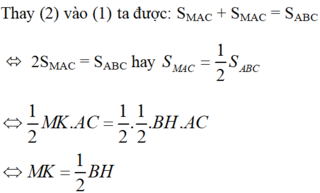
Do đó, M nằm trong ΔABC, nằm trên đường thẳng d bờ AC chứa B sao cho khoảng cách từ M đến AC = 1/2 đường cao BH.
Suy ra điểm M nằm trong ΔABC nằm trên đường trung bình của ΔABC.
Vẽ AH ^ BC, MK ^ BC
S M B C = S M A B + S M A C = 1 2 S A B C ⇒ M K = 1 2 A H
Vì M không nằm ngoài tam giác nên M nằm trên đoạn thẳng EF//BC và cách BC một khoảng (1/2) AH
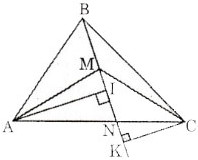
Theo giả thiết, M là điểm nằm trong tam giác ABC sao cho SMAC = SAMB + SBMC
Nhưng SAMB + SBMC + SMAC = SABC
Suy ra SMAC = SABC
∆ MAC = ∆ABC có chung đáy BC nên MK = 
BH. Vậy điểm M nằm trên đường trung bình EF của ∆ABC.
>>>>> Bí kíp học tốt các môn lớp 8 2017 bởi các Thầy C
Tham Khảo
3. Cho hình bình hành ABCD có AC > BD. Gọi H, K lần lượt là hình chiếu vuông góc của C trên đường thẳng AB và AD. Cmr
CH/CB=CK/CD
Tam giác CHK đồng dạng tam giác BCA
AB.AH + AD.AK= AC x AC
bài làm
![[IMG]](https://lh4.googleusercontent.com/-qw6b5CJV7g8/Ubnh5Fe6_uI/AAAAAAAAAJA/TOnMiHtG-S8/s475/unHM%252CJ%252Ctitled.GIF)
AO cắt BC tại I kẻ BE vg AI ,
CF vg AI Sabm= AO.BE/2 <= AO. BI/2
Cmtt S amc <= AM.CI/2
suy ra Sabmc <= AM.BC/2
Cmtt => Sabc<= AM.BC+BM.CA+CM.AB
dấu "=" xảy ra khi M là trực tâm
SAMB+SBMC=SMAC đặt là S1+S2=S3 và SABC=S
Ta có S1+S2+S3=S=> S1+S2=S-S3 = S3
=> S3/S=1/2
S và S3 có chung cạnh đáy AC => chiều cao ứng với AC cua S3 = 1/2 chiều cao ứng với AC của S
Vậy ta dựng đg cao BH ( H thuộc AC), lấy trung điểm M của BH, qua M vẽ đg thẳng d//BC cắt AB và AC tại O và P
=> điểm M nằm trên OP thì S1+S2=S3