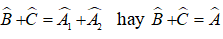Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì ba đường trung trực của tam giác đồng quy nên D thuộc đường trung trực của cạnh BC. Mặt khác đường trung trực của cạnh BC đi qua trung điểm của BC nên D là trung điểm của cạnh BC.
b) Ta có: Tam giác DEA = tam giác DEA (c.g.c) nên góc B = góc A1
<=> góc C = góc A2
=> Góc A = góc A1 + góc A2 = góc B + góc C.

a,tự vẽ hình ra nha!
Trên nửa mặt phẳng bờ BC ko chứa điểm A kẻ CH vug góc DH tại H sao cho DA=DH
Xét \(\Delta ABD\)và \(\Delta HBC\)có:
\(\widehat{A_1}=\widehat{H_1}\left(DA\perp AB,HD\perp HC\right)\)
DH=DA(theo cách vẽ)
\(\widehat{D_1}=\widehat{D_2}\)(đối đỉnh)
=> tam giác ABD= tam giác HCD(ch-gn)
=>DB=DC(2 cạnh t/ư)
=> D lak trung điểm của BC(đpcm)

B A C E F D 1 2 4 3
- Bài giải
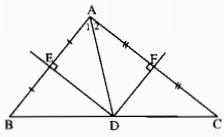
a) Gọi E là trung điểm của BA; F là trung điểm của AC
Nối A với D
+ Vì DE là đường trung trực của AB => DB = DA
+ Vì DF là đường trung trực của AC => DA = DC
Từ đó, suy ra : DB = DC
=> D là trung điểm của BC (Điều phải chứng minh)
b) Vì DB = DA (câu a)
-> \(\Delta\)BDA cân tại D
=> Góc B = Góc BAD
Vì DA = DC (câu a)
=> \(\Delta\)DAC cân tại D
=> Góc DAC = Góc C
=> Góc B + Góc C = Góc BAD + DAC
hay Góc B + góc C = góc A
(Điều phải chứng minh)
Chúc bạn học tốt !
Tham khảo:
a) Vì D là điểm chung của 2 dường trung trực
=>D là điểm chung của 3 đường trung trực (tính đồng quy trong tam giác)
=>D thuộc trung trực ứng với cạnh BC mà D thuộc BC
=> D là trung điểm của cạnh BC (đpcm)
b) Xét tam giác ADE và BDE có:
DE chung
DA = DB ( vì DE là đường trung trực của AB)
Suy ra: ∆ADE = ∆ BDE ( cạnh huyền – cạnh góc vuông).
+ Chứng minh tương tự ta có: ∆ADF = ∆ CDF ( cạnh huyền – cạnh góc vuông).
Từ (1) và (2) suy ra: