Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a/ Có AM= 3MB\(\Rightarrow\overrightarrow{AM}=3\overrightarrow{MB}\)
Theo quy tắc 3 điểm=> \(\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}\)
và \(\overrightarrow{CM}=\overrightarrow{CB}-\overrightarrow{MB}\)
Cộng vế vs vế=> \(2\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}+\overrightarrow{CB}-\overrightarrow{MB}\)
\(\Leftrightarrow2\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{MB}+\overrightarrow{CB}\)
\(\Leftrightarrow2\overrightarrow{CM}=\overrightarrow{CA}+\frac{2}{3}\overrightarrow{AB}+\overrightarrow{CB}\)
\(\Leftrightarrow6\overrightarrow{CM}=3\overrightarrow{CA}+2\overrightarrow{\:AB}+3\overrightarrow{CB}\)
\(\Leftrightarrow6\overrightarrow{CM}=\overrightarrow{CA}+5\overrightarrow{CB}\) ( vì \(2\overrightarrow{CA}+2\overrightarrow{AB}=2\overrightarrow{CB}\) )
b/ Làm tương tự câu a
c/ Theo quy tắc trung điểm có:
\(2\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{CB}\)
\(2\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{AC}\)
\(\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CB}=2\overrightarrow{AN}+\overrightarrow{BA}+2\overrightarrow{CM}+\overrightarrow{AC}\)
\(=2\overrightarrow{AN}+\overrightarrow{BC}+2\overrightarrow{CM}\)
Có \(\overrightarrow{BC}=2\overrightarrow{BN}=2\left(\overrightarrow{BA}+\overrightarrow{AN}\right)\)
=>\(\overrightarrow{AB}=2\overrightarrow{AN}+2\overrightarrow{BA}+2\overrightarrow{AN}+2\overrightarrow{CM}\)
\(\Leftrightarrow3\overrightarrow{AB}=4\overrightarrow{AN}+2\overrightarrow{CM}\Leftrightarrow\overrightarrow{AB}=\frac{4}{3}\overrightarrow{AN}+\frac{2}{3}\overrightarrow{CM}\)

A B C D I M
a)
\(\overrightarrow{AI}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AD}\right)=\dfrac{1}{2}\left(\overrightarrow{AB}+\dfrac{3}{4}\overrightarrow{AC}\right)=\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{8}\overrightarrow{AC}\).
b)
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}+x\overrightarrow{BC}\)\(=\overrightarrow{AB}+x\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=\left(1-x\right)\overrightarrow{AB}+x\overrightarrow{AC}\).
c) A, M, I thẳng hàng khi và chỉ khi hai véc tơ \(\overrightarrow{AM};\overrightarrow{AI}\) cùng phương
hay \(\dfrac{1-x}{\dfrac{1}{2}}=\dfrac{x}{\dfrac{3}{8}}\Leftrightarrow\dfrac{3}{8}\left(1-x\right)=\dfrac{1}{2}x\)
\(\Leftrightarrow\dfrac{7}{8}x=\dfrac{3}{8}\)\(\Leftrightarrow x=\dfrac{3}{7}\).

Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)
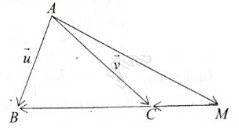
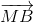 = 3
= 3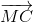 =>
=> 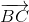 )
)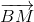 =
= 
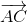 -
- 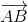 nên
nên 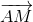 =
= 