Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔAMB và ΔKMC có
MA=MK
\(\widehat{AMB}=\widehat{KMC}\)
MB=MC
Do đó: ΔAMB=ΔKMC
b: Xét tứ giác BECF có
BE//CF
BE=CF
Do đó: BECF là hình bình hành
Suy ra: BC và EF cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của FE
hay F,M,E thẳng hàng

Lời giải:
a. Xét tam giác $AMC$ và $KMB$ có:
$MC=MB$ (do $M$ là trung điểm $BC$)
$AM=KM$ (gt)
$\widehat{AMC}=\widehat{KMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle KMB$ (c.g.c)
và $\widehat{ACM}=\widehat{KBM}$
Mà 2 góc này ở vị trí so le trong nên $AC\parallel BK$
b.
Xét tam giác $ABM$ và $KCM$ có:
$BM=CM$
$AM=KM$
$\widehat{AMB}=\widehat{KMC}$ (đối đỉnh)
$\Rightarrow \triangle ABM=\triangle KCM$ (c.g.c)
$\Rightarrow \widehat{ABM}=\widehat{KCM}$
Mà 2 góc này ở vị trí so le trong nên $AB\parallel CK$

Bạn kham khảo link này nhé.
Câu hỏi của Lê Minh Thảo - Toán lớp 7 - Học toán với OnlineMath


a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)

Hình cậu tự vẽ nhé!
Có tam giác ABC vuông tại A (góc A=90 độ)
suy ra CB^2=CA^2+AB^2(định lí py-ta-go)
CB^2=6^2+6^2
CB^2=36+36
CB^2=72
CB^2=
Câu này bạn chép sai đề à mk ko tính đc
b Xét tam giác AMB và tam giác AMC có
AB=AC(GT)
AM là cạnh chung
MB=CM(GT)
Suy ra tam giác AMB =tam giác AMC(TH c-c-c)
Phần còn lại cậu chép sai đề hay sao ý tớ ko chứm minh đc!

a,
Xét △ABC có:
BC2 = 172 = 289
AB2 + AC2 = 152 + 82 = 225 + 64 = 289
=> BC2 = AB2 + AC2
=> △ABC vuông
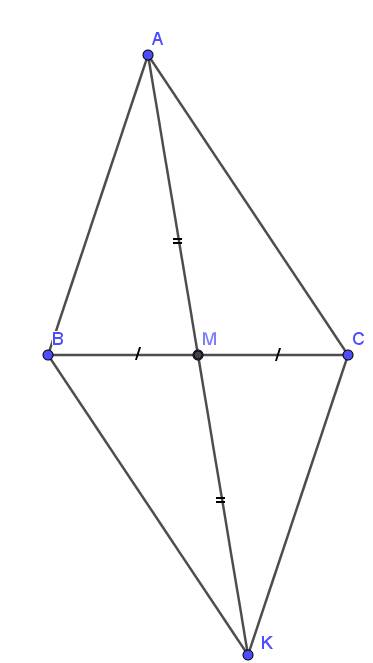
A B C K M 1 2 1 1
Xét \(\Delta AMB\) và \(\Delta KMC\) có :
AM = MK ( gt )
\(\widehat{M_1}=\widehat{M_2}\) 9 đối đỉnh )
BM = MC ( gt )
=> \(\Delta AMB\) = \(\Delta KMC\)
b)
\(\Delta AMB\) =\(\Delta KMC\)
\(\Rightarrow\widehat{B_1}=\widehat{C_1}\)
Mà góc B1 l C1 so le trong
=> BA // KC
có cả 9 đối đỉnh