

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Đáp án A
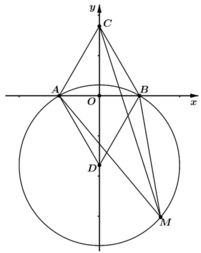
Chọn hệ trục Oxy sao cho Ox trùng với AB , chiều dương hướng từ A đến B ,trục Oy là đường trung trực của đoạn AB =>
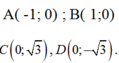
Phương trình đường tròn tâm D qua A; B là:
![]()
Giả sử M(a;b) là điểm bất kì trên đường tròn .Ta có :
MA2= (a+ 1) 2+ b2
MB2= (a-1) 2+ b2
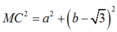

+ M nằm trên đường tròn (1) nên : 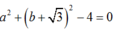
=> MA2+ MB2= MC2
=> MA; MB; MC là độ dài ba cạnh của một tam giác vuông.

Đáp án D
Ta có thể thấy ngay rằng các khẳng định A và C đều đúng.
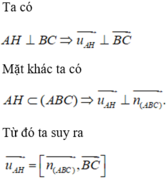
là một vectơ chỉ phương của đường thẳng AH.
Vậy D là khẳng định sai.

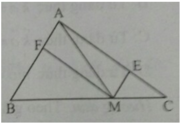
a;\(\overrightarrow{AB}+2\overrightarrow{AC}\)
\(=\overrightarrow{AM}+\overrightarrow{MB}+2\overrightarrow{AM}+2\overrightarrow{MC}\)
\(=3\overrightarrow{AM}\)
b: \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
\(=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\)
=3vecto MG

Chọn C.
Trong tam giác ABC có a = 6 nên BC = 6 mà BM = 3
suy ra M là trung điểm BC
Suy ra: ![]()

Đáp án D
Ta có:
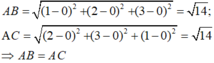
Ta thấy tam giác ABC cân tại đỉnh A. Do đó, AD đồng thời là đường cao của tam giác ABC nên các khẳng định A, B và C đều đúng.
Vậy khẳng định D sai.