Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)

\(\overrightarrow{CN}=2\overrightarrow{NA}\Leftrightarrow\overrightarrow{CA}+\overrightarrow{AN}=-2\overrightarrow{AN}\Leftrightarrow\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{AK}=\frac{1}{2}\overrightarrow{AM}+\frac{1}{2}\overrightarrow{AN}=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}\Rightarrow\overrightarrow{KA}=-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\)
\(\overrightarrow{KD}=\overrightarrow{KA}+\overrightarrow{AD}=\left(-\frac{1}{4}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AC}\right)+\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\right)\)
\(=\frac{1}{4}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\Rightarrow\left\{{}\begin{matrix}m=\frac{1}{4}\\n=\frac{1}{3}\end{matrix}\right.\) \(\Rightarrow m-n=-\frac{1}{12}\)

\(AM=\frac{1}{2}MB\Rightarrow\overrightarrow{AM}=\frac{1}{3}\overrightarrow{AB}\)
\(AN=3NC\Rightarrow\overrightarrow{AN}=\frac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{AK}=\frac{1}{2}\overrightarrow{AM}+\frac{1}{2}\overrightarrow{AN}=\frac{1}{2}.\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}.\frac{3}{4}\overrightarrow{AC}=\frac{1}{6}\overrightarrow{AB}+\frac{3}{8}\overrightarrow{AC}\)
\(\Rightarrow\left\{{}\begin{matrix}m=\frac{1}{6}\\n=\frac{3}{8}\end{matrix}\right.\) \(\Rightarrow mn=\frac{1}{16}\)

a;\(\overrightarrow{AB}+2\overrightarrow{AC}\)
\(=\overrightarrow{AM}+\overrightarrow{MB}+2\overrightarrow{AM}+2\overrightarrow{MC}\)
\(=3\overrightarrow{AM}\)
b: \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}\)
\(=\overrightarrow{MG}+\overrightarrow{GA}+\overrightarrow{MG}+\overrightarrow{GB}+\overrightarrow{MG}+\overrightarrow{GC}\)
=3vecto MG

\(\overrightarrow{CN}=2\overrightarrow{NA}\Leftrightarrow\overrightarrow{CA}+\overrightarrow{AN}=-2\overrightarrow{AN}\)
\(\Leftrightarrow-\overrightarrow{AC}=-3\overrightarrow{AN}\Rightarrow\overrightarrow{AN}=\frac{1}{3}\overrightarrow{AC}\)
\(\overrightarrow{AM}=\frac{1}{2}\overrightarrow{AB}\) (do M là trung điểm AB)
\(\overrightarrow{AK}=\frac{1}{2}\left(\overrightarrow{AM}+\overrightarrow{AN}\right)=\frac{1}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}\right)=\frac{1}{4}\overrightarrow{AB}+\frac{1}{6}\overrightarrow{AC}\)
\(\Rightarrow\left\{{}\begin{matrix}m=\frac{1}{4}\\n=\frac{1}{6}\end{matrix}\right.\)

Lời giải:
Lấy điểm $N$ trên $AB$ sao cho $MN\parallel AC$
Ta có:
\(\overrightarrow{AM}=\overrightarrow{AN}+\overrightarrow{NM}=\frac{AN}{AB}.\overrightarrow{AB}+\frac{NM}{AC}.\overrightarrow{AC}\)
Mà:
\(\frac{AN}{AB}=\frac{MC}{BC}; \frac{NM}{AC}=\frac{MB}{BC}\) theo định lý Ta-let với $MN\parallel AC$
\(\Rightarrow \overrightarrow{AM}=\frac{MC}{BC}\overrightarrow{AB}+\frac{MB}{BC}\overrightarrow{AC}\)
Ta có đpcm.

\(\overrightarrow{AJ}=\frac{3}{2}\overrightarrow{AM}=\frac{3}{2}\left(\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}\right)=\frac{3}{4}\overrightarrow{AB}+\frac{3}{4}\overrightarrow{AC}\)
\(\overrightarrow{JK}=\overrightarrow{JA}+\overrightarrow{AK}=-\overrightarrow{AJ}+\overrightarrow{AK}=-\frac{3}{4}\overrightarrow{AB}-\frac{3}{4}\overrightarrow{AC}+\frac{1}{4}\overrightarrow{AC}\)
\(=-\frac{3}{4}\overrightarrow{AB}-\frac{1}{2}\overrightarrow{AC}\Rightarrow\left\{{}\begin{matrix}m=-\frac{3}{4}\\n=-\frac{1}{2}\end{matrix}\right.\)

Ta có: \(\overrightarrow{MB}=3\overrightarrow{MC}\Rightarrow\overrightarrow{MB}=3\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow\overrightarrow{MB}=3\overrightarrow{MB}+3\overrightarrow{BC}\)
\(\Rightarrow-\overrightarrow{MB}=3\overrightarrow{BC}\)
\(\Rightarrow\overrightarrow{BM}=\dfrac{2}{3}\overrightarrow{BC}\). Mà \(\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}\) nên \(\overrightarrow{BM}=\dfrac{2}{3}\left(\overrightarrow{AC}-\overrightarrow{AB}\right)\)
Theo quy tắc 3 điểm, ta có
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\Rightarrow\overrightarrow{AM}=\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}-\dfrac{3}{2}\overrightarrow{AB}\)
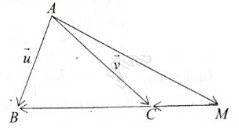
\(\Rightarrow\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{AB}+\dfrac{3}{2}\overrightarrow{AC}\) hay \(\overrightarrow{AM}=-\dfrac{1}{2}\overrightarrow{u}+\dfrac{3}{2}\overrightarrow{v}\)

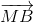 = 3
= 3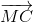 =>
=> 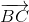 )
)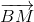 =
= 
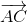 -
- 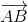 nên
nên 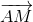 =
= 
\(\overrightarrow{MB}=-2\overrightarrow{MC}\Leftrightarrow\overrightarrow{MB}=-2\left(\overrightarrow{MB}+\overrightarrow{BC}\right)\)
\(\Rightarrow3\overrightarrow{MB}=-2\overrightarrow{BC}\Rightarrow\overrightarrow{BM}=\frac{2}{3}\overrightarrow{BC}=\frac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)=-\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}\)
\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}=\overrightarrow{AB}-\frac{2}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}=\frac{1}{3}\overrightarrow{AB}+\frac{2}{3}\overrightarrow{AC}\)
\(\Rightarrow\left\{{}\begin{matrix}m=\frac{1}{3}\\n=\frac{2}{3}\end{matrix}\right.\) \(\Rightarrow mn=\frac{2}{9}\)