Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) AK BC=M
AI BC = N
Tg ACM có CK là phân giác và đường cao => tg ACM cân => K trung điểm AM
Chứng minh tương tự với tg ABN => I trung điểm AN
Xét tg AMN có KI là đường trung bình => IK// MN => IK//BC
b) KI AB, AC lần lượt tại D, E
=> D và E lần lượt là trung điểm AB, AC
=> tg AKC vuông có trung truyến thuộc cạnh huyền => KE=1/2 AC
và tg AIB vuông có trung tuyến thuộc cạnh huyền => ID=1/2 AB
mà DE=1/2 BC => KD= KE- DE =1/2(AC-BC)
EI=DI-DE=1/2(AB-BC)
mKI=KD+DE+EI=1/2(AC-BC+AB-BC+BC)= 1/2(AC+AB-BC)
k mk nha!!

a) Gọi E là giao điểm của AK với BC. F là giao điểm của AI với BC.
- cm được: tam giác AKC=tam giác EKC (ch-gn).
=> AK=KE ; AC=CE.
- cm được: tam giác ABI=tam giác FBI (ch-gn).
=>AI=FI ; AB=BF.
Xét tam giác AEF có AK=KE và AI=IF
=>IK là đtb tam giác AEF
=>IK // EF ; IK=EF/2
=>IK // BC
b) Tớ sẽ tính IK cho bạn theo dạng tổng quát.
Đặt AB=c; AC=b;BC=a.
Ta có AC = CE = b ; AB = BF = c
Ta có CE + BF = BE + EF + EF + CF = EF +BC
=> b + c = EF + a
=>EF = b + c - a
mà IK = EF/2
=>IK = (b+c-a)/2

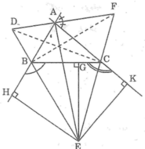
Ta có: AE là tia phân giác góc trong tại đỉnh A
AF là tia phân giác góc ngoài tại đỉnh A
Suy ra: AE ⊥ AF (tính chất hai góc kề bù)
Vậy AE ⊥ DF.

Ta có: EH = EK (chứng minh trên)
Suy ra: E thuộc tia phân giác của ∠(BAC).
Mà E khác A nên AE là tia phân giác của ∠(BAC)