Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=BH\cdot CH\)
\(\Leftrightarrow AH^2=4\cdot9=36\)
hay AH=6(cm)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BC=4+9=13(cm)
Ta có: ΔABC vuông tại A(gt)
mà AM là đường trung tuyến ứng với cạnh huyền BC(M là trung điểm của BC)
nên \(AM=\dfrac{1}{2}BC\)(Định lí 1 về áp dụng hình chữ nhật vào tam giác vuông)
hay \(AM=\dfrac{1}{2}\cdot13=6.5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAMH vuông tại H, ta được:
\(AM^2=AH^2+MH^2\)
\(\Leftrightarrow MH^2=AM^2-AH^2=6.5^2-6^2=6.25\)
hay MH=2,5(cm)
Diện tích tam giác AMH là:
\(S_{AMH}=\dfrac{AH\cdot HM}{2}=\dfrac{6\cdot2.5}{2}=\dfrac{15}{2}=7.5\left(cm^2\right)\)

a,
Xét Δ AHB và Δ CAB, có :
\(\widehat{AHB}=\widehat{CAB}=90^o\)
\(\widehat{ABH}=\widehat{CBA}\) (góc chung)
=> Δ AHB ∾ Δ CAB (g.g)
=> \(\dfrac{AH}{CA}=\dfrac{HB}{AB}\)
=> \(\dfrac{AB}{CA}=\dfrac{HB}{AH}\)
Xét Δ AHB và Δ CHA, có :
\(\widehat{AHB}=\widehat{CHA}=90^o\)
\(\dfrac{AB}{CA}=\dfrac{HB}{AH}\) (cmt)
=> Δ AHB ∾ Δ CHA (g.g)
=> \(\dfrac{AH}{CH}=\dfrac{HB}{HA}\)
=> \(AH^2=HB.CH\)
b, Ta có : \(AH^2=BH.CH\) (cmt)
=> \(AH^2=4.9\)
=> \(AH^2=36\)
=> AH = 6
Xét Δ AHB, có :
\(AB^2=AH^2+BH^2\)
=> \(AB^2=6^2+4^2\)
=> \(AB^2=52\)
=> AB = 7,2 (cm)
Xét Δ AHC, có :
\(AC^2=AH^2+CH^2\)
=> \(AC^2=6^2+9^2\)
=> \(AC^2=117\)
=> AC = 10,8 (cm)
Xét Δ ABC, có :
\(BC^2=AB^2+AC^2\)
=> \(BC^2=7,2^2+10,8^2\)
=> \(BC^2=168,48\)
=> BC = 12,9 (cm)
Ta có : MC = \(\dfrac{1}{2}BC\) (M là trung điểm BC do có đường trung tuyến AM)
=> MC = 6,45 (cm)
Ta có : BC = BH + HM + MC
=> 12,9 = 4 + HM + 6,45
=> HM = 12,9 - 4 - 6,45
=> HM = 2,45 (cm)
Xét Δ AMH vuông tại H, có :
\(S_{\Delta AMH}=\dfrac{1}{2}AH.HM\)
=> \(S_{\Delta AMH}=\dfrac{1}{2}.6.2,45\)
=> \(S_{\Delta AMH}=7,35\left(cm\right)\)

Xét hai tam giác vuông HBA,HAC có:
∠ (BHA) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ ∠ C )
⇒ △ HBA đồng dạng △ HAC (g.g)
Suy ra: 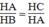
⇒ H A 2 = HB.HC = 4.9 = 36(cm)
Suy ra: AH = 6(cm)
Lại có: BM = 1/2 BC = 1/2 .(9+4) = 1/2 .13 = 6,5cm
Mà HM = BM – BH = 6,5 – 4 = 2,5cm
Vậy S A H M = 1/2 AH.HN = 1/2 .6.2,5 = 7,5 c m 2

a)
Ta có \(\Delta ABC\approx\Delta HBA\)vì hai tam giác vuông này có chung góc nhọn B
Lại có \(\Delta ABC\approx\Delta HAC\)có chung góc nhọn C
\(\Rightarrow\Delta HBA\approx\Delta HAC\)(tính chất bắc cầu)
b)Ta có AM là trung tuyến nên \(BM=\frac{1}{2}\left(BH+CH\right)=\frac{13}{2}\)
\(HM=BM-BH=\frac{13}{2}-4=\frac{5}{2}\)
Vì \(\Delta HBA\approx\Delta HAC\)nên
\(\frac{HB}{HA}=\frac{HA}{HC}\Rightarrow\frac{4}{HA}=\frac{HA}{9}\)
\(\Rightarrow HA^2=36\Rightarrow HA=6\)
\(S_{ABC}=\frac{\frac{5}{2}\cdot6}{2}=\frac{15}{2}\left(cm^2\right)\)

a, đồng dạng trường hợp góc - góc
b, Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền nên ta có :
AM = BM = CM = BC/2 = (BH + CH )/ 2 = 13/2 = 6,5 ( cm )
ta có : HM = BM - BH = 6,5 - 4 = 2,5 ( cm )
áp dụng định lí Pytago cho tam giác vuông AHM ta có : \(AH^2=AM^2-HM^2\Rightarrow AH=\sqrt{AM^2-HM^2}=\sqrt{6,5^2-2,5^2}=6.\) (cm )
\(S_{AMH}=\frac{AH.HM}{2}=\frac{6.2,5}{2}=7,5\left(cm^2\right)\)

Ta có BH=4 ; CH=9 =>BC = 13
Vì AM là đường trung tuyến nên AM = MC = BC/2 = 6.5
Ta có HM = BC-( BH + MC ) = 2,5
lại có AM là đường trung tuyến nên AM = BC/2 = 6,5
Xét tam giác vuông AHM : AH^2 = AM^2 - HM^2
=>. AH = 6
S tam giác AMH = 1/2.AH.HM = 7,5
──────▄▌▐▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▀▌
───▄▄██▌█ ░Xe chở 100000000 đến đây..
▄▄▄▌▐██▌█ ░░░░░░ ░░░░░░░░░ ░░░░░░░▐\.
███████▌█▄▄▄▄▄▄ ▄▄▄▄▄▄▄▄▄▄▄▄▄▄▄ ▄▄▌ \.
▀❍▀▀▀▀▀▀▀❍❍▀▀▀▀ ▀▀▀▀▀▀▀▀▀▀▀❍❍ ▀▀.
░░░░░░███████ ]▄▄▄▄▄▄▄▄▃
▂▄▅█████████▅▄▃▂
I███████████████████].
◥⊙▲⊙▲⊙▲⊙▲⊙▲⊙▲⊙◤…
Bằng chíu

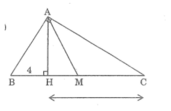
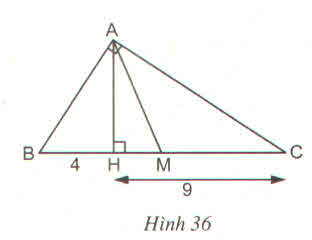


BC = BH + CH = 13 (cm)
∆ABH ~ ∆CAH (g.g)
=> AH² = BH . CH = 36
=> AH = 6
BM = 1/2 BC = 6,5 (cm)
=> HM = 2,5 (cm)
Do đó S_(AHM) = 1/2 . 2,5 . 6 = 7,5 (cm²)
Đề thiếu! cho mỗi góc bẹt sao tính bạn