Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ MN//AC ~> N là trg điểm của AB và MN=1/2 AC
Gọi giao điểm của MN và BI là E
tam giác ABM có trọng tâm E nên EM=2/3 MN
~> EM=1/3 AC
Tam giác ADI=MEI ~> AD=ME ~> AD=1/3AC
chúc bạn học tốt
Từ M kẻ MK//DE ,MKcắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)

Từ M kẻ MK//DE ,MKcắt AC tại K
Xét tg AMK có:
DE//MK
D là tr.điểm AM
=>E là tr.điểm AK
=>AE=EK=1/2AK
Xét tg BEC có:
BE//MK (do DE//MK)
M là tr.điểm BC (AM là tr.tuyến của tg ABC)
=>K là tr.điểm EC
=>KE=1/2EC
Mà AE=EK (cmt)
=>AE=1/2EC (đpcm)

Xét ΔBEC có
M là trung điểm của BC
F là trung điểm của EC
Do đó: MF là đường trung bình của ΔBEC
Suy ra: MF//DE
Xét ΔAMF có
D là trung điểm của AM
DE//MF
Do đó: E là trung điểm của AF
Suy ra: AE=EF
mà EF=FC
nên AE=FE=FC
hay \(AE=\dfrac{EC}{2}\)

Gọi K là trung điểm của EC
Xét ΔBEC có
M là trung điểm của BC(gt)
K là trung điểm của EC(Gt)
Do đó: MK là đường trung bình của ΔBEC
Suy ra: MK//BE
hay MK//DE
Xét ΔAMK có
D là trung điểm của AM(Gt)
DE//MK(cmt)
Do đó: E là trung điểm của AK(Định lí 1 đường trung bình của tam giác)
Suy ra: AE=EK
mà EK=KC
nên AE=EK=KC
\(\Leftrightarrow AE=\dfrac{EK+KC}{2}=\dfrac{EC}{2}\)

Giải
Ta thấy đường trung bình tam giác ABC nên BEDC là hình thang, lại có\(BM=MC\cdot DN=NC\Rightarrow MN\) là đường trung bình hình thang BEDC hay MN ong song DE và BC. Lại dùng đường trung bình thì
\(MI=KN=\frac{DE}{2}\left(1\right)\)
\(MN=\frac{DE^2+BC}{2}\Rightarrow IK=MN-2MI=\frac{DE+BC}{2}-DE\)
\(=\frac{BC-DE}{2}=\frac{DE^2}{2}\left(BC=2DE\right)\left(2\right)\)
\(\Leftrightarrow Q\cdot E\cdot D\Rightarrowđcpm\)
![[IMG]](http://d.f10.photo.zdn.vn/upload/original/2012/07/09/20/02/1341838952939363106_574_0.jpg)
Mình sẽ làm câu b trước rồi từ đó suy ra a
b)Giả sử MP=PQ=QN đã có từ trước
Xét △△ ABC có E là trung điểm AB,D là trung điểm AC \Rightarrow ED là đường trung bình của △△ ABC\Rightarrow ED//BC và ED=BC/2(*)
Xét hình thang EDBC có M là trung điểm BE,N là trung điểm CE \Rightarrow MN//BC( (*) (*) )
Từ (*)( (*) (*) ) \Rightarrow ED//MN
Xét △△ BED có M là trung điểm BE,MP//ED \Rightarrow MP là đường trung bình của △△ BED \Rightarrow MP=ED/2
Tương tự cũng có NQ=ED/2
Ta có :MP=PQ
\Leftrightarrow ED2=BC−ED2ED2=BC−ED2
\Leftrightarrow ED=BC-ED
\Leftrightarrow 2ED=BC
Tương tự với NQ và PQ cũng rứa
Vậy muốn NQ=PQ=MP thì 2ED=BC Điều này là hiển nhiên ở (*)
từ đó phát triển lên câu a)NQ=PQ=MP=1/2ED
\Rightarrow MN=3/2ED \RightarrowMN=3/4BC
Đúng thì thanks giùm nha

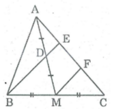
Gọi F là trung điểm của EC.
Trong ∆ CBE, ta có:
M là trung điểm của CB;
F là trung điểm của CE.
Nên MF là đường trung bình của ∆ CBE
⇒ MF// BE (tính chất đường trung bình của tam giác) hay DE// MF
* Trong ∆ AMF, ta có: D là trung điểm của AM
DE // MF
Suy ra: AE = EF (tính chất đường trung bình của tam giác)
Mà EF = FC = EC/2 nên AE = 1/2 EC

bài 1 làm sao vậy sao ko thấy mấy câu trả lời vậy bạn giúp mình giải bài tập số 1 với cảm ơn nhiều