Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a)xet tam giac abd va tam giac aed co
ab=ae
ad la canh chunggoc bad = goc ead
=>tam giác abd = ead
b)gọi i là giao điểm của ad và be
xét tam giác abi và tam giác aei có :
ab=ae
ad là cạnh chung
goc bai = góc eai
=> tam giác abi= tâm giác aei
=>ib=ie =>ad là đường trung trực của be
cho mk 3 đi mk giải tiếp cho, bài nay mk vừa mới kiểm tra
mk giải tiếp nè
theo câu a,b=>góc dbf= góc dec (kề bù do góc abd= aed)
xét tam giác bfd và ecd có
góc dbf= góc dec
bd=ed
bdf=edc
=> tam giác dbf= tam giác ecd
k cho mk đi.mk hứa mk tl hết cho mà
tự kẻ hình nghen:3333
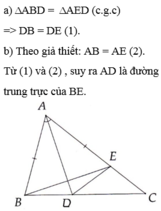
a) xét tam giác ABD và tam giác AED có
A1=A2(gt)
AD chung
AB=AE(gt)
=> tam giác ABD= tam giác AED(cgc)
=> BD=DE( hai cạnh tương ứng)
b) vi AD cắt BE tại K
xét tam giác ABK và tam giác AEK có
A1=A2(gt)
AK chung
AB=AE(gt)
=> tam giác ABK= tam giác AEK(cgc)
=> BK=EK( hai cạnh tương ứng)
=> AKB=AKE( hai góc tương ứng)
mà AKB+AKE=180 độ(kề bù)
=> AKB=AKE=180/2=90 độ
=> AD là trung trực của BE
c) ta có AD vuông góc với BE (AKB= 90 độ)
=> AB^2=AK^2+BK^2 (áp dụng định lý pytago)
=> AE^2=AK^2+EK^2 (áp dụng định lý pytago)
=> BD^2=BK^2+KD^2 (áp dụng định lý pytago)
=> DC^2=DE^2+KD^2( áp dụng định lý pytago)
=> AB^2+DE^2=AK^2+EK^2+DK^2+BK^2
=> AE^2+BD^2=AK^2+EK^2+DK^2+BK^2
=> AB^2+DE^2=AE^2+BD^2
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó:ΔABD=ΔAED
Suy ra: DB=DE
b: Ta có: AB=AE
DB=DE
Do đó: AD là đường trung trực của BE
Hình tự vẽ
Chứng minh
Gọi giao điểm của AD và BE là F
Vì AD là phân giác của góc ABC => góc BAD=góc CAD
Xét tam giác BAF và tam giác CAF :
AB=AB(gt)
góc BAD=góc CAD(cmt)
ÀF chung
=> Tam giác BAF = tam giác CAF(c.g.c)
=>BF=CF( hai cạnh tương ứng) (*)
góc BFA = góc CFA ( hai góc tương ứng) (1)
mà góc BFA + góc CFA = 180 độ ( 2 góc kề bù) (2)
Từ (1) và (2) => góc BFA = góc CFA = 90 độ =>AD vuông góc với BE(**)
Từ (*) và (**) => AD là trung trực BE (ĐPCM)
Chắc đề đây này:
Bài 4. Cho tam giác ABC có AB < AC và phân giác AD (D ∈ BC). Trên AC lấy điểm E sao cho AE = AB. Trên tia AB lấy điểm F sao cho AC = AF. Chứng minh:
a) DB = DE ; BF = CE
b) Ba điểm F , D , E thẳng hàng
c) BE // FC ; AD \(\perp\) FC
a: Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
Suy ra DB=DE
Ta có: AB+BF=AF
AE+EC=AC
mà AF=AC
và AB=AE
nên BF=EC
b: Xét ΔBDF và ΔEDC có
BF=EC
\(\widehat{DBF}=\widehat{DEC}\)
BD=DE
Do đó: ΔBDF=ΔEDC
Suy ra: \(\widehat{BDF}=\widehat{EDC}\)
=>\(\widehat{BDF}+\widehat{BDE}=180^0\)
=>E,D,F thẳng hàng
c: Xét ΔAFC có
AB/AF=AE/AC
nên BE//FC
Ta có: ΔACF cân tại A
mà AD là đường phân giác
nên AD là đường cao
a,
xét tam giác ABD và tam giác ADE có
AB=AE (gt)
GÓC A1= GÓC A2 ( ad là tia phân giác)
ad chung
=> tam giác abd = tam giác ade (c.g.c)
b, xét tam giác BAI và tam giác EAI có:
AB=AE(gt)
A1=A2 (ad là tia phân giác)
AI chung
=> tam giác BAI = tam giác EAI (c.g.c)
=> BI=IE (2 cạnh t,ứng)
vì BI=BE ( cmt) => AI là đường trung trực của BE
P/s: 2 phần kia bạn tự làm nhé ak cái I là BE cắt AD tại I
