Cho tam giác ABC đường cao AH,BI,CK CMR AH.BC=CK.AB=BI.CA

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Nam Trần

20 tháng 11 2017

Cho tam giác ABC đường cao AH,BI,CK CMR

AH.BC=CK.AB=BI.CA

#Toán lớp 8

Kien Nguyen

20 tháng 11 2017

Diện tích tam giác

Đúng(0)

Kien Nguyen

20 tháng 11 2017

Hỏi đáp Toán

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Dzung PQ

16 tháng 4 2017 - olm

Câu hỏi hay

Cho tam giác nhọn ABC, O là giao điểm ba đường cao AH, BI, CK. Cmr: \(\frac{OH}{AH}\)+ \(\frac{OI}{BI}\) + \(\frac{OK}{CK}\)= 1

#Toán lớp 8

alibaba nguyễn

18 tháng 4 2017

Ta có:

\(\frac{OH}{AH}+\frac{OI}{BI}+\frac{OK}{CK}=\frac{\frac{OH.BC}{2}}{\frac{AH.BC}{2}}+\frac{\frac{OI.AC}{2}}{\frac{BI.AC}{2}}+\frac{\frac{OK.AB}{2}}{\frac{CK.AB}{2}}\)

\(=\frac{S_{BOC}}{S_{ABC}}+\frac{S_{COA}}{S_{ABC}}+\frac{S_{AOB}}{S_{ABC}}=\frac{S_{ABC}}{S_{ABC}}=1\)

Đúng(0)

Vũ Như Mai

19 tháng 4 2017

Đường cao không cần kí hiệu vuông góc ạ?!

Đúng(0)

Hồ Tiến Đức

11 tháng 7 2017

Cho tam giác nhọn ABC, O là giao điểm ba đường cao AH, BI, CK. Cmr: \(\dfrac{OH}{AH}+\dfrac{OI}{BI}+\dfrac{OK}{CK}=1\)

#Toán lớp 8

Ngô Thanh Sang

11 tháng 7 2017

Ta có:

\(\dfrac{OH}{AH}+\dfrac{OI}{BI}+\dfrac{OK}{CK}=\dfrac{\dfrac{OH.BC}{2}}{\dfrac{AH.BC}{2}}+\dfrac{\dfrac{OI.AC}{2}}{\dfrac{BI.AC}{2}}+\dfrac{\dfrac{OK.AB}{2}}{\dfrac{CK.AB}{2}}\)

\(=\dfrac{S_{BOC}}{S_{ABC}}+\dfrac{S_{COA}}{S_{ABC}}+\dfrac{S_{AOB}}{S_{ABC}}=\dfrac{S_{ABC}}{S_{ABC}}=1\)

Hok tốt

Đúng(0)

Đức Hiếu

11 tháng 7 2017

Nhầm trầm trọng tam giác không vuông anh à

Đúng(0)

Nguyễn Vũ Xuân Vân

29 tháng 4 2017 - olm

Cho tam giác ABC vuông tại A biết AB=6cm, AC=8cm. Kẻ đường cao AH (H thuộc BC).

a. Tính BC.

b. Chứng minh tam giác ABC đồng dạng tam giác HBA

c. Chứng minh AB.AC = AH.BC

d. Từ H kẻ HI vuông góc AB (I thuộc AB) và HK vuông góc AC (K thuộc AC). Chứng minh \(\dfrac{AB^3}{AC^3}=\dfrac{BI}{CK}\)

#Toán lớp 8

minh chuong

29 tháng 4 2017

tự làm nhé

bài đó dễ quá nên mik ko biết làm

Đúng(0)

Trần Thị Quế

29 tháng 4 2017

bạn nói dễ mà sao ko biết làm minh chuong

Đúng(0)

Trần trọng nam

14 tháng 5 2015 - olm

Cho tam giác ABC vuông tại A. AH là đường cao; H thuộc BC. BD là phân giác góc B (D thuộc AD).

a, CMR: tam giác ABD đồng dạng tam giác ABH; tam giác AHC đồng dạng tam giác BAC.

b, CMR: AH.BC=AC.BA.

c, gọi K là giao điểm của AH và BD. CMR: tam giác AKD can tại A

#Toán lớp 8

Nguyễn Thị Ngọc Mai

12 tháng 3 2019 - olm

Cho tam giác ABC vuông tại A , AB=6cm, AC=8cm, kẻ đường cao AH

a, Cmr AH.BC=AB.AC

b, Gọi M,N lần lượt là hình chiếu của AH trên AB,AC. Cmr tâm giác AMN đồng dạng với tam giác ACB

c, Tính diện tích BMNC

#Toán lớp 8

Pham Trong Bach

13 tháng 1 2017

Cho tam giác ABC vuông tại A, đường cao AH. Chứng minh:

AH.BC = AB.AC

#Toán lớp 8

Cao Minh Tâm

13 tháng 1 2017

S = A B C 1 2 A H . B C = 1 2 A B . A C

Þ AH.BC = AB.AC (ĐPCM)

Đúng(0)

Đặng Kiều Anh

26 tháng 6 2017 - olm

Cho tam giác ABC có AB= 5 cm; AC= 12 cm; BC= 13 cm. Vẽ đường cao AH, đường trung tuyến AM (H, M thuộc BC) và MK vuông góc AC. Chứng minh

a/ tam giác ABC vuông

b/ tam giác AMC cân

c/ tam giác AHB đồng dạng tam giác AKM

d/ AH. BM= CK.AB

#Toán lớp 8

Nguyễn Hữu Minh

19 tháng 3 2022

cho tam giác abc vuông tại a, đường cao ah. a) Chứng minh: ah.bc = ab.ac, b) be là tia phân giác góc abc, be cắt ah tại d. chứng minh. tam giác abd đồng dạng tam giác cbe

#Toán lớp 8

Nguyễn Lê Phước Thịnh

14 tháng 1

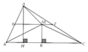
a: Xét ΔABC có AH là đường cao

nên \(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC\left(1\right)\)

Ta có: ΔABC vuông tại A

=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC\left(2\right)\)

Từ (1) và (2) suy ra \(AH\cdot BC=AB\cdot AC\)

b: Xét ΔABD và ΔCBE có

\(\widehat{ABD}=\widehat{CBE}\)(BE là phân giác của góc ABC)

\(\widehat{BAD}=\widehat{BCE}\left(=90^0-\widehat{ABC}\right)\)

Do đó: ΔABD~ΔCBE

Đúng(0)

Doãn Thùy Dung

3 tháng 8 2015 - olm

Cho tam giác ABC cân tại A( góc A tù). Các đường cao BI và CK cắt nhau tại D.a, Chứng minh tam giác BDC cân.b, Gọi H lag chân đường cao AH của tam giác ABC. Chứng minh D, A, H thẳng hàng

#Toán lớp 8

Nguyễn Thị Huệ

3 tháng 8 2015

bạn kẻ hình giúp mk nha!

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP