Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: AC=4cm; AB=3cm
a: \(S_{ABC}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
BD là phân giác
=>AD/AB=CD/BC
=>AD/3=CD/5=(AD+CD)/(3+5)=4/8=0,5
=>AD=1,5cm; CD=2,5cm
\(BD=\sqrt{1.5^2+3^2}=\dfrac{3}{2}\sqrt{5}\left(cm\right)\)

a: XétΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
DO đó: ΔABC\(\sim\)ΔHBA
b: Ta có: ΔABC\(\sim\)ΔHBA
nên BA/BH=BC/BA
hay \(BA^2=BH\cdot BC\)

Hình vẽ bạn phải tự vẽ được chứ, bài này là bài rất rất rất cơ bản rồi đấy:vv
Ta có tam giác ABC là tam giác vuông
=> SABC=\(\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.4.3=6\) (cm2)
Áp dụng định lý Py-ta-go vào tam giác vuông ABC:
BC2=AB2+AC2=42+32=52
=> BC=5(cm)
Mà SABC=\(\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.AH.5=2,5.AH=6\)
=> AH=2,4(cm)
Vậy...
Có thể do cẩu thả mình sai số chỗ nào đó nhưng hướng làm như này nhé, đáng nhẽ bài này mình không giải đâu:vv

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A
Ta có: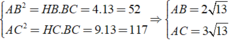
Vậy S A B C = 1 2 A B . A C = 1 2 . 2 13 . 3 13 = 39 c m 2
Chọn đáp án A.

a: Xét ΔAHC vuông tại Hvà ΔHKC vuông tại K có
góc C chung
=>ΔAHC đồng dạng với ΔHKC
b: Xet ΔHAC vuông tại H có HK là đường cao
nên HK^2=AK*KC
c: \(S_{AHC}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
\(AC=\sqrt{3^2+4^2}=5\left(cm\right)\)
CK=4^2/5=3,2cm
=>AK=1,8cm
=>HK=2,4cm
\(S_{HKC}=\dfrac{1}{2}\cdot2.4\cdot3.2=1.2\cdot3.2=3.84\left(cm^2\right)\)

a: Xét ΔAHC vuông tại Hvà ΔHKC vuông tại K có
góc C chung
=>ΔAHC đồng dạng với ΔHKC
b: Xet ΔHAC vuông tại H có HK là đường cao
nên HK^2=AK*KC
c: \(S_{AHC}=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
\(AC=\sqrt{3^2+4^2}=5\left(cm\right)\)
CK=4^2/5=3,2cm
=>AK=1,8cm
=>HK=2,4cm
\(S_{HKC}=\dfrac{1}{2}\cdot2.4\cdot3.2=1.2\cdot3.2=3.84\left(cm^2\right)\)
6cm2
\(\text{Diện tích tam giác là}:S=\dfrac{AH.BC}{2}=\dfrac{3.4}{2}=\dfrac{12}{2}=6\left(cm^2\right)\)