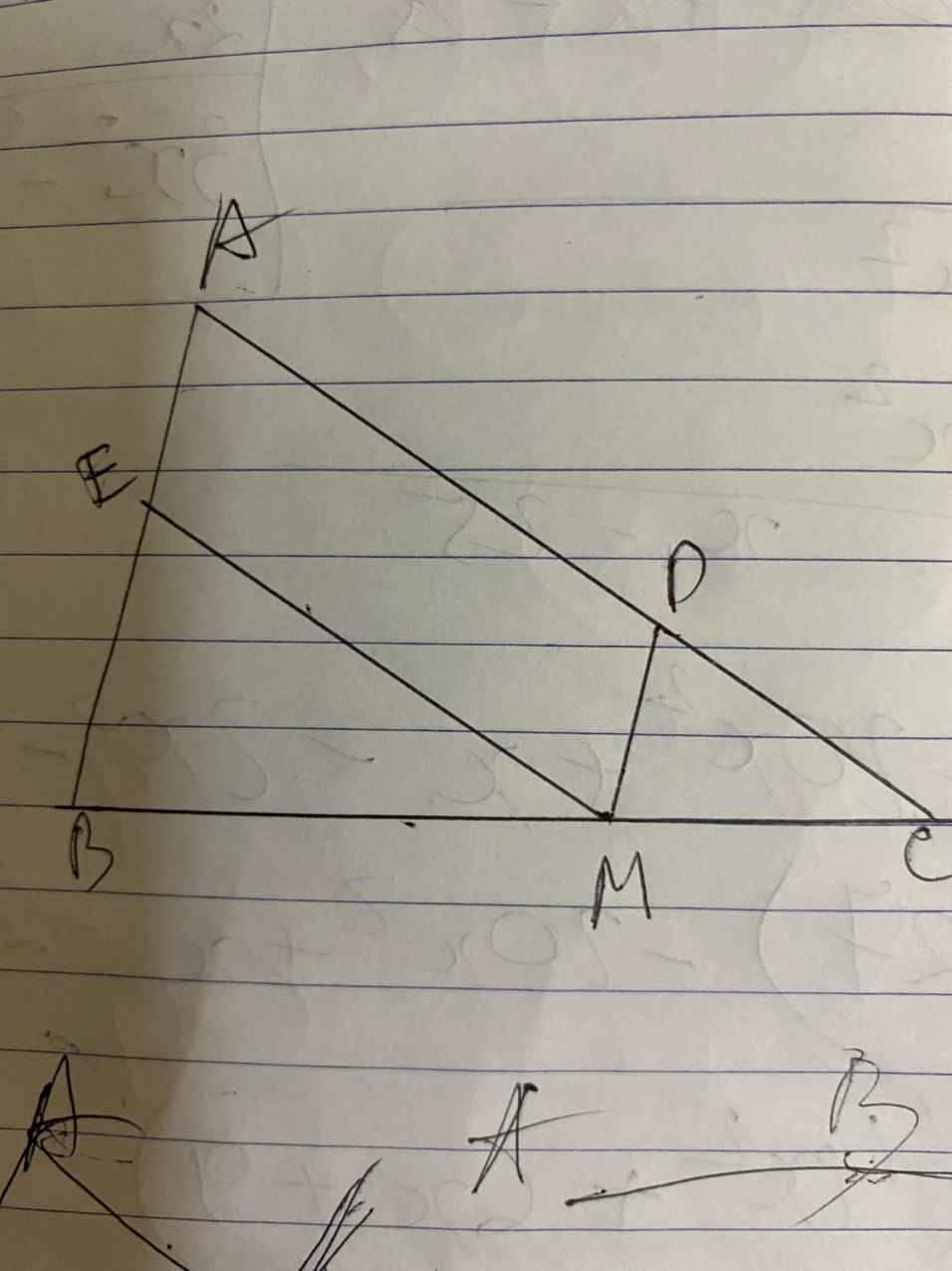Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{GIẢI :}\)
A B C M D E
a) Xét \(\diamond\text{ADME}\) có \(DM\text{ }//\text{ }AB\), \(EM\text{ }//\text{ }AC\) \(\Rightarrow\text{ }\diamond\text{ADME}\) là hình bình hành.
b) Để hình bình hành ADME là hình thoi \(\Leftrightarrow\text{ }AM\) là tia phân giác của góc A.
Vậy M là giao điểm của tia phân giác góc A và cạnh BC thì ADME là hình thoi.
c) Để hình bình hành ADME là hình chữ nhật \(\Leftrightarrow\angle\text{A}=90^0\text{ }\Leftrightarrow\text{ }\bigtriangleup\text{ABC}\) vuông tại A.

\(\text{GIẢI :}\)
A B C M E D
Chứng minh :
a) Xét \(\diamond\text{AEMD}\), có \(\hept{\begin{cases}\text{AE // DM }\\\text{EM // AD}\end{cases}}\)
\(\Rightarrow \text{ }\diamond\text{AEMD}\) là hình bình hành.
b) Để hình bình hành AEMD là hình thoi \(\Rightarrow\) AM là đường phân giác của góc A.
c) Để hình bình hành AEMD là hình vuông \(\Rightarrow\text{ }\hept{\begin{cases}\bigtriangleup\text{ABC vuông tại A}\\\text{AM là đường phân giác góc A}\end{cases}}\).

TL:
a,G là trọng tâm của tam giác ABC nên GD =1/2 BG suy ra GM= GD
Tương tự EG=GN suy ra MNDE là hình bình hành
a) Trong tam giác ABC , có :
EA = EB ( CE là trung tuyến )
DA = DC ( DB là trung tuyến )
=> ED là đường trung bình của tam giác ABC
=> ED // BC (1) , DE = 1/2 BC (2)
Trong tam giác GBC , có :
MG = MB ( gt)
NG = NC ( gt)
=> MN là đương trung bình của tam giác GBC
=> MN // BC (3) , MN = 1/2 BC (4)
Từ 1 và 2 => ED // MN ( * )
Từ 3 và 4 => ED = MN ( **)
Từ * và ** => EDMN là hbh ( DHNB )

a) BD, CE là các đường trung tuyến của \(\Delta ABC\)
\(\Rightarrow\)DA = DC; EA =EB
\(\Rightarrow\)ED là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)ED // BC; ED = 1/2 BC
\(\Delta GBC\)có MG = MB; NG = NC
\(\Rightarrow\)MN là đường trung bình của \(\Delta GBC\)
\(\Rightarrow\)MN // BC; MN = 1/2 BC
suy ra: MN // ED; MN = ED
\(\Rightarrow\)tứ giác MNDE là hình bình hành
c) MN = ED = 1/2 BC
\(\Rightarrow\)MN + ED = \(\frac{BC}{2}\)+ \(\frac{BC}{2}\)= BC

Hih e tự vẽ nha:
a) Vì DM//BE nên tứ giác BDME là hình thang.
Lại có :\(\widehat{B}=\widehat{C}=60\)( tam giác ABC đều)
và \(\widehat{BEM}=\widehat{C}=60\)(Vì DE//AC và ACB=90 độ)
=>\(\widehat{BEM}=\widehat{B}=60\)
=>Tứ giác BDME là htc.
T/tự cho các hình còn lại.
b)Xét tam giác BDM và EMD:
BD=ME( BDME là htc)
góc BDM=góc EMD(Vì DM//BE và góc BEM=góc B=60 độ)
DM là cah chug
=> tg BDM=tg EMD (cgc)
=>BM=DE
C/m t/tự đối vói các tg AFD=AMF; tg CEM=tg FME
=> AM=DF;CM=EF
=>BM+AM+CM=DE+DF+EF= Chu vi của tam giác DEF
c) Ở câu a/ ta đã có góc B= góc E=60 nên suy ra đc các góc còn lại của htc BDME bằng 120 độ
T/tự cho 2 htc còn lại suy ra đc cả 3 góc đều =120 độ nên chúng = nhau
M A B C D E F
a, Chứng minh các tứ giác BDME,CFME,ADMF là các hình hang cân.
Ta có : MD//BC\(\Rightarrow\)BDME là hình thang cân .(1)
ME//AC\(\Rightarrow\widehat{MEB}=\widehat{ACB}\)(hai góc đồng vị )
mà \(\widehat{ACB}=\widehat{ABC}=60^o\)(do tam giác ABC đều)
\(\Rightarrow\widehat{MEB}=\widehat{ABC}=60^o\)(2)
Từ (1) và (2) => tứ giác BDME là hình thang cân.
Chứng minh tương tự ta cũng có : tứ giác CFME và ADMF là các hình thang cân.
b,Chứng minh chu vi của tam giác DEF bằng tổng các khoảng cách từ M đến các đỉnh của tam giác ABC . \(\left(P_{DME}=MB+MA+MC\right)\)
Ta có : \(P_{DEF}=DE+DF+EF\)
Lại có tứ giác BDME là hình thang cân (cmt) => DE = MB.
tứ giác CFME là hình thang cân (cmt)=> MC=EF
tứ giác DMF là hình thang cân (cmt)=> MA =DF.
\(\Rightarrow P_{DEF}=MA+MB+MC\)
=> đpcm.
c,Chứng minh \(\widehat{DME}=\widehat{DMF}=\widehat{EMF}\)
Trong hình thang cân BDME có : \(\widehat{DBE}=60^o\)
mà \(\widehat{DME}+\widehat{DBE}=180^o\Rightarrow\widehat{DME}=180^o-\widehat{DBE}=180^o-60^o=120^o\)
Chứng minh tương tự ta có : \(\widehat{DMF}=120^o;\widehat{EMF}=120^o\)
=>\(\widehat{DME}=\widehat{DMF}=\widehat{EMF}=120^o\)(đpcm)
Mình giải chi tiết rùi đấy nhé nếu có j hk hiểu cứ nhắn tin cho mk mk sẽ giải thích cho nhé.
Nên nhớ hình vẽ chỉ mang tính chất minh họa . Mình vẽ hình cho mấy bạn nhìn vô cho dể hiểu thôi chứ chưa chuẩn lắm đâu mấy bạn tự vẽ hình cho đẹp nhé ai thấy hay thì k cho mk nhé . CẢM ƠN NHIỀU .
a) xét tứ giác ADME có DM//AE ; ME//AD
⇒ ADME là hbh
b) nếu tứ giác ADME là hình thoi ⇒ đg chéo AM là đường phân giác của góc A
Vậy điểm M là chân đương phân giác của góc A thi ADME là hình thoi
c) theo câu (a) ADME là hbh , ADME là hình chữ nhật thì khi đó góc A=90
⇒ABC là tam giác vuông tại A