Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C E M d
gọi d là đường phân giác của góc ngoài tại C trên tia đối của tia Cb lấy E sao cho CE=CA
vì tam giác ACE cân tại C d là đường phân giác của góc ACE nên d là đường trung trực của AEdo đó MA=ME
ta có AC+CB=EC+CB=BE
AM+MB=EM+MB
tâm giác BME có BE<EM+MB
=> AC+CB<AM+MB
mk chỉ có thể vẽ hình minh họa


Từ A kẻ đường vuông góc với tia pg của góc ngoài đỉnh C và cắt tia đối của tia CB tại A'.
Cm được MA = MA', CA = CA'.
Theo BĐT trong tam giác MBA' : MA' + MB > BA' = BC + CA' = BC + AC ⇒⇒ MA + MB > BC + AC (đpcm)

Từ A kẻ đường vuông góc với tia pg của góc ngoài đỉnh C và cắt tia đối của tia CB tại A'.
Cm được MA = MA', CA = CA'.
Theo BĐT trong tam giác MBA' : MA' + MB > BA' = BC + CA' = BC + AC ⇒⇒ MA + MB > BC + AC (đpcm)

A B C M N x
Trên tia đối của tia CB lấy điểm N sao cho AC = CN
Ta thấy Cx là tia phân giác ^ACN; M thuộc Cx => ^ACM = ^NCM
Xét \(\Delta\)ACM và \(\Delta\)NCM có: CA=CN; ^ACM = ^NCM; CM chung => \(\Delta\)ACM = \(\Delta\)NCM (c.g.c)
=> MA = MN (2 cạnh tương ứng)
Xét \(\Delta\)MBN có: MN + MB > BN (BĐT tam giác) => MN + MB > CN + CB (1)
Thay MA = MN (cmt); AC = CN vào (1) => MA + MB > AC + CB (đpcm).
Cho tam giác ABC. Điểm M nằm trên đường phân giác của góc ngoài đỉnh C. Chứng minh AC + CB < AM + MB

Trên tia đối của tia CB lấy điểm A' sao cho CA' = CA. Sử dụng tính chất của tam giác cân ta có được CM là đường trung trực của AA' Þ MA = MA'. Sử dụng bất đẳng thức trong tam giác A'MB ta có: CA + CB = CA' + CB = BA' <MA' + MB Þ CA + CB < MA + MB.
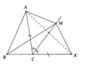

A B C M E c
Gọi Cc là tia phân giác ngoài đỉnh C
Trên tia đổi của CB lấy điểm E sao cho AC = EC
=> \(\Delta ACE\)cân tại C
Mà Cc là tia phân giác của góc \(\widehat{ACE}\)
=> Cc vừa là Tia phân giác vừa là đường trung trực của AE
=> MA = ME ( tc)
Ta có \(AC+CB\Leftrightarrow EC+CB\left(AC=EC\right)=BE\left(1\right)\)
\(AM+BM\Leftrightarrow ME+BM\left(2\right)\)
Xét tam giác BME có
\(BE< ME+BM\left(dl\right)\left(3\right)\)
Từ (1); (2) và (3)
\(\Rightarrow AC+BC< AM+BM\left(đpcm\right)\)

Kẻ \(AH\perp MC\)cắt BC ở K
Xét hai tam giác vuông AHC và KHC có:
HC: cạnh chung
\(\widehat{ACH}=\widehat{KCH}\)(gt)
Suy ra \(\Delta AHC=\Delta KHC\left(cgv-gnk\right)\)
\(\Rightarrow AH=KH\) và AC = KC (hai cạnh tương ứng)
Xét hai tam giác vuông AMH và KMH có:
MH: cạnh chung
\(AH=KH\)(cmt)
Suy ra \(\Delta AMH=\Delta KMH\left(2cgv\right)\)
\(\Rightarrow AM=KM\)(hai cạnh tương ứng)
Áo dụng BĐT tam giác vào tam giác BMK, ta được: \(BM+MK>BK\)
\(\Rightarrow BM+AM>BC+CK\)
\(\Rightarrow BM+AM>BC+AC\left(đpcm\right)\)

A B C M D H
Từ A vẽ AH vuông góc với CM cắt BC tại D.
\(\Delta MAH=\Delta MDH\left(cgc\right)\)(tự chứng minh)
\(=>MA=MD\)(2 cạnh tương ứng)
Theo bất đẳng thức tam giác : MD+MB>BD
nên MA+MB>BD (1)
Ta có : BD=BC+CD
Mà CA=CD(tự chứng minh)nên BD=CA+CB(2)
Từ (1) và (2) => CA+CB<MA+MB
Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ∆ ACE cân tại C có CM là đường phân giác nên CM là đường trung trực (tính chất tam giác cân)
⇒ MA = ME (tính chất đường trung trực)
Ta có: AC + BC = CE + BC = BE (1)
MA + MB = ME + MB (2)
Trong ∆ MBE, ta có: BE < MB+ ME (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB.