Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

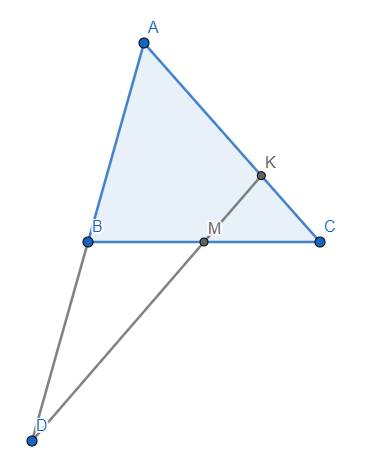
Bài này có thể giải bằng cách dùng định lý Menelaus khá ngắn như sau:
Áp dụng định lý Menelaus cho tam giác ABC với cát tuyến DMK, ta có: \(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{AB}=1\) \(\Rightarrow1.\dfrac{KC}{KA}.2=1\) \(\Leftrightarrow\dfrac{KC}{KA}=\dfrac{1}{2}\) \(\Leftrightarrow KA=2KC\) (đpcm)
Nhưng nếu bạn chưa được dùng định lý Menelaus thì sẽ phải làm như sau:
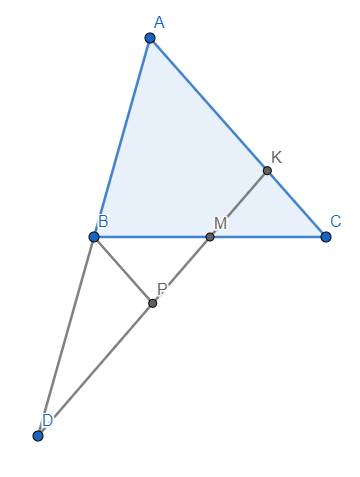
Kẻ BP//AC \(\left(P\in DK\right)\). Khi đó theo định lý Thales, \(\dfrac{MB}{MC}=\dfrac{BP}{CK}\) và \(\dfrac{DA}{DB}=\dfrac{AK}{BP}\). Do đó:
\(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{DB}=\dfrac{BP}{CK}.\dfrac{CK}{AK}.\dfrac{AK}{BP}=1\), và tới đây ta lại quay về tính như đã trình bày ở trên.

Qua B kẻ BH // AC , cắt DM tại H
Ta có {BH // AK ; AB = BD => BH là đường trung bình của tam giác ADK
=> AK=2BH (1)
Dễ dàng chứng minh được tam giác MKC = tam giác MBH (g.c.g)
=> BH = CK (2)
Từ (1) và (2) suy ra AK = 2CK
Qua B Kẻ BH // AC , cắt DM tại H
Ta có : BH // AK
AB // BD
=> BH là đường trung bình của tam giác ADK
=> AK = 2 BH (1)
· * Xét tam giác MKC và tam giác MBH .
CÓ : BM = CM ( M là trung điểm của BC)
Góc M1= Góc M2 ( 2 góc đối đỉnh)
Góc MKC = MBH ( = 90 *)* là độ
=> Tam giác MKC = Tam giác MBH ( g. c . g)
=> BH = KC ( 2 cạnh tương ứng )(2)
Từ (1), (2) suy ra được AK = 2 KC

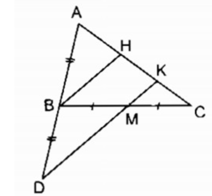
Gọi H là trung điểm của AK
Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.
⇒ BH // DK (tính chất đường trung bình của tam giác)
Hay BH // MK
Trong ∆ BCH ta có M là trung điểm của BC
MK // BH
⇒ CK = HK
AK = AH + HK = 2HK
Suy ra: AK = 2 KC ( vì HK =KC)

Gọi H là trung điểm của AK
Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.
⇒ BH // DK (tính chất đường trung bình của tam giác)
Hay BH // MK
Trong ∆ BCH ta có M là trung điểm của BC
MK // BH
⇒ CK = HK
AK = AH + HK = 2HK
Suy ra: AK = 2 KC ( vì HK =KC)

A B C M K D H
Qua B kẻ BH // AC , cắt DM tại H
Ta có \(\begin{cases}BH\text{//}AK\\AB=BD\end{cases}\) => BH là đường trung bình của tam giác ADK
=> AK=2BH (1)
Dễ dàng chứng minh được \(\Delta MKC=\Delta MBH\left(g.c.g\right)\)
=> BH = CK (2)
Từ (1) và (2) suy ra AK = 2CK
Gọi H là trung điểm của AK
=>BH là đtb của tam giác ADK
=> BH//MK
mà M là trung điểm của BC
=>HK=KC
=> AH=HK=KC
=> AK=2KC
lm ik mik cho like nak bài dễ mak