Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi \(M\left(x;y\right)\Rightarrow\left(x+3\right)^2+\left(y+4\right)^2=1\)
\(\left\{{}\begin{matrix}\overrightarrow{MA}=\left(1-x;2-y\right)\\\overrightarrow{MB}=\left(-2-x;1-y\right)\\\overrightarrow{MC}=\left(3-x;4-y\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=\left(2-3x;7-3y\right)\)
\(T^2=\left(3x-2\right)^2+\left(3y-7\right)^2\)
Đặt \(\left(x+3;y+4\right)=\left(a;b\right)\Rightarrow a^2+b^2=1\)
\(T^2=\left(3a-11\right)^2+\left(3b-19\right)^2\)
\(T^2=9\left(a^2+b^2\right)-66a-114b+482=491-6\left(11a+19b\right)\)
Ta lại có:
\(\left(11a+19b\right)^2\le\left(11^2+19^2\right)\left(a^2+b^2\right)=482\)
\(\Rightarrow11a+19b\ge-\sqrt{482}\)
\(\Rightarrow T^2\le491+6\sqrt{482}\)
\(\Rightarrow T\le\sqrt{491+6\sqrt{482}}\)
Số liệu bài toán cho xấu 1 cách phi lý và vô nghĩa
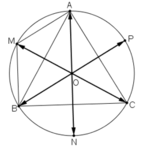
a)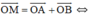 
M là đỉnh còn lại của hình bình hành AOBM.
+ AOBM là hình bình hành ⇒ AM = OB
Mà OB = OA (= bán kính đường tròn) ⇒ AM = AO ⇒ ΔAMO cân tại A (1)
+ AOBM là hình bình hành ⇒ AM//BO
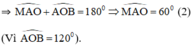
Từ (1) và (2) ⇒ ΔAMO đều ⇒ OM = OA ⇒ M nằm trên đường tròn ngoại tiếp ΔABC.
Mà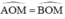 
nên M là điểm chính giữa cung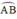 
b) Chứng minh tương tự phần a) ta có: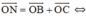 
N là điểm chính giữa cung BC.
c)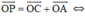 
P là điểm chính giữa cung CA.