Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC và AB=EC
c: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔBCD cân tại C
d: Xét ΔOBC có
OM là đường cao
OM là đường trung tuyến
Do đó: ΔOBC cân tại O
Suy ra: OB=OC(1)
Xét ΔOBD có
OA là đường cao
OA là đường trung tuyến
Do đó: ΔOBD cân tại O
Suy ra: OB=OD(2)
Từ (1) và (2) suy ra OB=OC=OD
hay O cách đều ba đỉnh của ΔBDC


a) Xét tam giác AMB và tam giác DMC có:
BM = CM (gt)
AM =DM (gt)
\(\widehat{AMB}=\widehat{DMC}\) (Hai góc đối đỉnh)
\(\Rightarrow\Delta AMB=\Delta CMD\left(c-g-c\right)\)
b) Do \(\Delta AMB=\Delta CMD\Rightarrow\widehat{BAM}=\widehat{DCM}\)
Chúng lại ở vị trí so le trong nên AB //CD.
c) Xét tam giác AME có MH là đường cao đồng thời trung tuyến nên tam giác AME cân tại M.
Suy ra MA = ME
Lại có MA = MD nên ME = MD.
d) Xét tam giac AED có MA = ME = MD nê tam giác AED vuông tại E.
Suy ra ED // BC
Xét tam giác cân MED có MK là trung tuyến nên đồng thời là đường cao.
Vậy thì \(MK\perp ED\Rightarrow MK\perp BC\)

a) Xét: "tam giác" ABM và "tam giác" EMC có:
- AM = ME ( gt )
- BM = CM ( gt )
- "góc" AMB = "góc" CME ( đối đỉnh )
=> "Tam giác" ABM = "Tam giác" EMC ( c.g.c )
b) Ta có: "tam giác" AMB = "Tam giác" EMC nên "góc" BAM = "góc" AEC
Mặt khác: hai góc BAM và AEC nằm ở vị trị so le trong
=> AB // CE
c) Xét : "tam giác" AIB và "tam giác" CIK có:
- AI = IC ( gt )
- BI = IK ( gt )
- "góc" AIB = "góc" CIK ( đối đỉnh )
=> "tam giác" AIB = " tam giác" CIK ( c.g.c )
=> "góc" BAI = "góc" KCI ( 2 góc tương ứng )
=> KC // AB
Theo tiên đề ơ- clit về hai đường thẳng song song thì qua một điểm nằm ngoài một đường thẳng có một và chỉ một đường thẳng song song với đường thẳng đó:
Mà: AB // CE (theo b) và KC // AB (cmt)
Nên: E, K, C thẳng hàng
____________________ End _________________________
Mình nghĩ vậy ... không biết có đúng không :) còn mấy chữ nằm trong ngoặc kép ( " " ) bạn thay bằng kí hiệu nha, mình không biết viết kí hiệu ...... hì hì

Lời giải:
a. Xét tam giác $AMC$ và $EMB$ có:
$AM=ME$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{AMC}=\widehat{EMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle EMB$ (c.g.c)
$\Rightarrow AC=EB$
b. Xét tam giác $AFD$ và $BED$ có:
$FD=ED$
$AD=BD$ (do $D$ là trung điểm $AB$)
$\widehat{ADF}=\widehat{BDE}$ (đối đỉnh)
$\Rightarrow \triangle AFD=\triangle BED$ (c.g.c)
$\Rightarrow AF=BE$
Mà theo phần a thì $AC=BE$ nên $AF=AC$

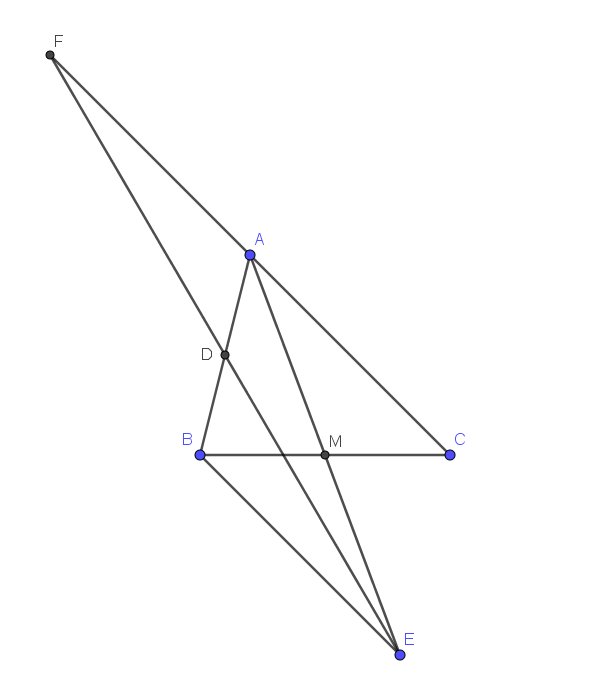
Gọi O là giao điểm của AD và BC
=>O là trung điểm của AD
Xét ΔADE có
O là trung điểm của AD
M là trung điểm của AE
Do đó OM là đường trung bình
=>OM//DE
hay DE//BC
Xét ΔCAD có
CO là đường cao
CO là đường trung tuyến
DO đó: ΔCAD cân tại C
=>CA=CD(1)
Xét tứ giác ABEC có
M là trung điểm của AE
M là trung điểm của BC
Do đó: ABEC là hình bình hành
Suy ra: BE=AC(2)
Từ (1) và (2) suy ra BE=CD
Xét tứ giác BDEC có DE//BC
nên BDEC là hình thang
mà BE=CD
nên BDEC là hình thang cân
=>BD=CE

Xét tam giác AMC và tam giác EMB
có: \(\widehat{AMC}=\widehat{BME}\)(đối đỉnh)
BM = MC (gt)
AM = ME (gt)
=> tam giác AMC = tam giác EMB (c.g.c)
=> AC = BE (1); và \(\widehat{ACB}=\widehat{CBE}\)
Xét tam giác ADF và tam giac BDE
có: \(\widehat{FDA}=\widehat{BDE}\) ((đối đỉnh)
FD = DE (gt)
AD = DB (gt)
=> tam giác ADF = tam giác BDE (c.g.c)
=> AF = BE (2) và \(\widehat{FAD}=\widehat{DBE}\)
Từ (1) và (2) => AF = AC
Ta lại có: \(\widehat{FAB}+\widehat{BAC}=\widehat{ABE}+\widehat{BAC}=\widehat{ABC}+\widehat{CBE}+\widehat{BAC}=\widehat{ABC}+\widehat{BAC}+\widehat{ACB}=180^0\)
=> F, A, C thẳng hàng
=> A là trung điểm của FC

a: Xét tứ giác ACEB có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ACEB là hình bình hành
Suy ra: AC//BE