Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM
câu a có bạn bên trên là rồi nên mình sẽ làm câu b nha bạn ^^
b) Vì tam giác ABC cân có MA phân giác => MA vuông BC và M trung điểm BC. Vì MA = MD nên M trung điểm AD.
Xét tứ giác ABDC có M trung điểm AD và BC => hình bình hành
=> AB = CD, AB // CD

a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM

a: Xét ΔABM và ΔACM có
AM chung
AB=AC
BM=CM
Do đó: ΔABM=ΔACM
b: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
c: Xét tứ giác ABDC có
M là trung điểm của BC
M la trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//CD

a) Xét \Delta AMBΔAMB và \Delta DMCΔDMC có:
AB=AC(gt)
AM=MD(gt)
MB=MC(gt)
=>\Delta AMB=\Delta DMC\left(c.c.c\right)ΔAMB=ΔDMC(c.c.c)
b) Vì: \Delta AMB=\Delta DMC\left(cmt\right)ΔAMB=ΔDMC(cmt)
=> \widehat{MAB}=\widehat{MDC}MAB=MDC . Mà hai góc này ở vị trí sole trong
=>AB//DC
# Study well 'v'
a) Xét \(\Delta AMB\) và \(\Delta DMC\) , ta có:
AB = AC (gt)
AM=MD (gt)
MD=MC (gt)
\(\Rightarrow\Delta AMB=\Delta DMC\left(c.c.c\right)\)
b) Vì: \(\Delta AMB=\Delta DMC\left(cmt\right)\)
\(\Rightarrow\widehat{MAB=\widehat{MDC}}\)
\(\Rightarrow AB\) // \(DC\)
#Chúc bạn học tốt ^^

1 Xét 2 tam giác MAB và tam giác MDC:
Ta thấy:
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
BM=MC (gt)
MA=MD (gt)
Từ các giả thiết trên, suy ra:
\(\Delta MAB=\Delta MDC\left(c-g-c\right)\)

Ôi xin lỗi nhé,nhưng mình không hiểu cái đề bài cho lắm!

a. Xét △ABM và △DCM:
\(AM=MD\left(gt\right)\)
\(\hat{AMB}=\hat{DMC}\) (đối đỉnh)
\(BM=MC\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
b. Từ a. => \(\hat{MCD}=\hat{MBA}\) (2 góc tương ứng). Mà hai góc này ở vị trí so le trong
\(\Rightarrow CD\text{ // }AB\left(a\right)\)
c. Xét △CIK và △AIB:
\(AI=IC\left(gt\right)\)
\(\hat{AIB}=\hat{CIK}\) (đối đỉnh)
\(BI=IK\left(gt\right)\)
\(\Rightarrow\Delta CIK=\Delta AIB\left(c.g.c\right)\Rightarrow\hat{ICK}=\hat{IAB}\). Mà hai góc ở vị trí so le trong
\(\Rightarrow AB\text{ // }CK\left(b\right)\)
Từ (a) và (b), theo tiên đề Ơ-clit \(\Rightarrow AB\text{ // }DK\)
Vậy: D, C, K thẳng hàng (đpcm).
a) Xét tam giác ABM và tam giác DCM:
BM = CM (M là trung điểm BC).
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh).
MA = MD (cmt).
\(\Rightarrow\) Tam giác ABM = Tam giác DCM (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{CDM}\) (Tam giác ABM = Tam giác DCM).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) CD // AB (dhnb).
c) Xét tứ giác AKCB có:
I là trung điểm AC (gt).
I là trung điểm BK (IB = IK).
\(\Rightarrow\) Tứ giác AKCB là hình bình hành (dhnb).
\(\Rightarrow\) CK // AB (Tính chất hình bình hành).
Mà CD // AB (cmt).
\(\Rightarrow\) D, C, K thẳng hàng.


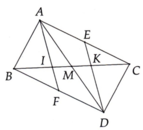
Giúp mik vs
a: Xét ΔABM và ΔACM có
AB=AC
\(\widehat{BAM}=\widehat{CAM}\)
AM chung
Do đó: ΔABM=ΔACM