Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

BTS là cục cứt chó j , nó đéo xứng làm cục cứt của the coconut tao
con kia là đồ giả mạo
Mà ông Duy có j hay đâu mà bọn m giả lắm thế

làm câu a thôi nha
A B C H K
a) trên tia HB lấy HK sao cho HK = HC
xét tam giác ACH và tam giác AKH có :
AH ( cạnh chung )
\(\widehat{AHC}=\widehat{AHK}=90^o\)
HC = HK ( theo cách vẽ )
suy ra : tam giác ACH = tam giác AKH ( c.g.c )
=> HC = HK ( hai cạnh tương ứng )
=> \(\widehat{C}=\widehat{AKH}\)( hai góc tương ứng )
=> AC = AK ( hai cạnh tương ứng )
tam giác AKB có \(\widehat{AKH}\)là góc ngoài tại đỉnh K có :
\(\widehat{AKH}\)= \(\widehat{KAB}+\widehat{B}\)
Mà \(\widehat{C}=2.\widehat{B}\)hay \(\widehat{AKH}\)= \(2.\widehat{B}\)
\(\Rightarrow2.\widehat{B}=\widehat{KAB}+\widehat{B}\)
\(\Rightarrow\widehat{KAB}=\widehat{B}\)
=> tam giác KAB cân tại K
=> KA = KB
=> AC + CH = KB + HK = BH
b)

Bài 1:
a: XétΔABE và ΔACD có
AB=AC
\(\widehat{BAE}\) chung
AE=AD
Do đó: ΔABE=ΔACD
Suy ra: BE=CD
b: Xét ΔDBC và ΔECB có
DB=EC
BC chung
DC=EB
Do đó: ΔDBC=ΔECB
Suy ra: \(\widehat{KDB}=\widehat{KEC}\)
Xét ΔKDB và ΔKEC có
\(\widehat{KDB}=\widehat{KEC}\)
BD=CE
\(\widehat{KBD}=\widehat{KCE}\)
Do đó: ΔKDB=ΔKEC

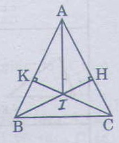
a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra ˆIAKIAK^=ˆIAHIAH^
Vậy AI là tia phân giác của góc A.
a) Hai tam giác vuông ABH và ACH có:
Tam giác ABC cân tại A ⇒ AB = AC
AH cạnh chung.
Nên ∆ABH = ∆ACH(Cạnh huyền – cạnh góc vuông)
Suy ra HB = HC
b)∆ABH = ∆ACH (Câu a)
Suy ra ∠BAH = ∠CAH (Hai góc tương ứng)

Câu hỏi của duyvodich10 - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại đây nhé.

Bài làm
a) Xét tam giác ABM có:
MK là đường trung trực
=> MB = MA ( tính chất đường trung trực )
=> Tam giác ABM cân tại M
b) Vì MK vuông góc AB
CB vuông góc AB
=> MK // CB
=> ^AMK = ^MCB ( đồng vị ). (1)
Vì tam giác ABM cân tại M
Mà MK là trung trực
=> MK là phân giác
=> ^AMK = ^BMK. (2)
Từ (1) và (2) => ^BMK = ^MCB. (3)
Vì tam giác BMK vuông tại K
=> ^BMK + ^MBK = 90°
Vì tam giác ABC vuông tại A
=> ^MBK + ^MBC = 90°
=> ^BMK = ^MBC. (4)
Từ (3) và (4) => ^MBC = ^MCB
bài làm
c) Xét tam giác BIA có:
AH vuông góc với BI
IK vuông góc với AB
Mà AH và IK cắt nhau ở M
=> M là trực tâm
=> BM vuông góc với IA ( đpcm )
d) Xét tam giác HMB và tam giác EMA có:
^MHB = ^MEA = 90°
Cạnh huyền: BM = AM ( cmt )
Góc nhọn: ^HMB = ^EMA ( đối )
=> Tam giác HMB = tam giác EMA ( ch-gn )
=> HM = ME
=> Tam giác MHE cân tại M
=> ^MHE = ^MEH
Xét tam giác MHE có:
^HME + ^MHE + ^MEH = 180°
=> ^HME + 2^MHE = 180°
=> 2^MHE = 180° - ^HME. (5)
Xét tam giác ABM cân tại M có:
^BMA + ^MBA + ^MAB = 180°
=> ^BMA + 2^MAB = 180°
=> 2^MAB = 180° - ^BMA. (6)
Mà ^HME = ^BMA ( đối ). (7)
Từ (5) và (6) và (7) => 2^MHE = 2^MAB
=> ^MHE = ^MAB
Mà hai góc này ở vị trí so le le trong
=> HE // AB
A B C K K' H
Ta có: \(AC-AB>CK-BH\) (*)
\(\Leftrightarrow AC+BH>AB+CK\)
\(\Leftrightarrow\left(AC+BH\right)^2>\left(AB+CK\right)^2\)
\(\Leftrightarrow AC^2+BH^2+2.AC.BH>AB^2+CK^2+2.AB.CK\)
\(\Leftrightarrow AC^2+BH^2+4S_{ABC}>AB^2+CK^2+4S_{ABC}\)
\(\Leftrightarrow AC^2+BH^2>AB^2+CK^2\)
\(\Leftrightarrow AK>AH\) (**)
Xét tam giác ABC có \(\widehat{B}>\widehat{C}\Rightarrow AC>AB\)
Trên AC lấy điểm B' sao cho AB' = AB \(\Rightarrow AB'< AC\Rightarrow\) B' nằm giữa A và C. (1)
Kẻ B'K' vuông góc AB tại K'.Suy ra B'K' // KC (2)
Từ (1) và (2) suy ra K' nằm giữa A và K hay AK' < AK
Ta thấy ngay \(\Delta ABH=\Delta ACK'\) (Cạnh huyền - góc nhọn)
\(\Rightarrow AH=AK'\Rightarrow AK>AH\)
Vậy (**) đúng hay (*) đúng.
A B C K H
Ta có tam giác AKC vuông tại K
=> AC là cạnh lớn nhất (nhận xét quan hệ giữa cạnh đối diện với góc lớn hơn)
=>AC > CK
Ta có tam giác ABH vuông tại H
=> AB là cạnh lớn nhất (nhận xét quan hệ giữa cạnh đối diện với góc lớn hơn)
=> AB > BH
Có: AC>CK;
AB>BH (cmt)
=> AC-AB > CK-BH