Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C H D
Bài làm:
a) Xét 2 tam giác: \(\Delta ABC\)và \(\Delta HBA\)có:
\(\hept{\begin{cases}\widehat{ABC}chung\\\widehat{AHB}=\widehat{BAC}=90^0\end{cases}}\)
=> \(\Delta ABC\)đồng dang với \(\Delta HBA\)(G.G)
b) \(\Delta AHB\)đồng dạng với \(\Delta CAB\)(G.G) vì:
\(\hept{\begin{cases}\widehat{AHB}=\widehat{AHC}=90^0\\\widehat{BAH}=\widehat{ACH}=90^0-\widehat{HAC}\end{cases}}\)
=> \(\frac{BH}{AH}=\frac{AH}{HC}\)\(\Leftrightarrow AH^2=BH.HC\)
c) Vì tam giác ABC vuông tại A nên theo định lý Py-ta-go, ta có:
\(BC^2=AB^2+AC^2=6^2+8^2=100\Rightarrow BC=10\left(cm\right)\)
Theo phần a, \(\Delta ABC\)đồng dạng với \(\Delta HBA\)(G.G)
=> \(\frac{BA}{AH}=\frac{BC}{AC}\Rightarrow AH=\frac{AB.AC}{BC}=\frac{48}{10}=4.8\left(cm\right)\)
Mà theo phần b, \(AH^2=BH.HC\)\(\Leftrightarrow BH.HC=4.8^2=23.04\Leftrightarrow HC=\frac{23.04}{HB}\)
Thay vào ta có: \(HB+HC=BC\)
\(\Leftrightarrow HB+\frac{23.04}{HB}=10\)
Từ đó ta giải phương trình ẩn HB ra, \(HB=3.6\left(cm\right)\)
=> \(HC=10-3.6=6.4\left(cm\right)\)
d) Đề bạn viết nhầm phải là cho AD là phân giác của tam giác ABC.
Áp dụng tính chất của tia phân giác trong tam giác ta có:
\(\frac{BD}{DC}=\frac{AB}{AC}=\frac{3}{4}\Leftrightarrow DC=\frac{4}{3}BD\)
Thay vào đó, ta giải phương trình sau:
\(BD+DC=BC\Leftrightarrow BD+\frac{4}{3}BD=10\)
Từ đó ta giải phương trình ẩn BD => \(BD=\frac{30}{7}cm\)
=> Diện tích tam giác ABD là:
\(S\Delta ABD=\frac{AH.BD}{2}=\frac{4.8\times\frac{30}{7}}{2}=\frac{72}{7}\left(cm^2\right)\)
Học tốt!!!!

A B C H 1 2
a) Xét tam giác ABC và tam giác HBA có:
\(\hept{\begin{cases}\widehat{B}chung\\\widehat{BAC}=\widehat{BHA}=90^0\end{cases}\Rightarrow\Delta ABC~\Delta HBA\left(g.g\right)}\)(3)
b) Vì tam giác BHA vuông tại H(gt) nên \(\widehat{B}+\widehat{A1}=90^0\)( 2 góc bù nhau ) (1)
Ta có: \(\widehat{A1}+\widehat{A2}=\widehat{BAC}=90^0\)(2)
(1),(2)\(\Rightarrow\widehat{B}=\widehat{A2}\)
Xét tam giác HBA và tam giác HAC có:
\(\hept{\begin{cases}\widehat{B}=\widehat{A2}\\\widehat{BHA}=\widehat{AHC}=90^0\end{cases}\Rightarrow\Delta HBA~\Delta HAC\left(g.g\right)}\)(4)
\(\Rightarrow\frac{AH}{BH}=\frac{CH}{AH}\)( các đoạn tương ứng tỉ lệ )
\(\Rightarrow AH^2=BH.CH\)(5)
c) Áp dụng định lý Py-ta-go vào tam giác ABC vuông tại A ta có:
\(AB^2+AC^2=BC^2\)
\(\Rightarrow BC=\sqrt{AB^2+AC^2}=10\)(cm)
Từ (3) \(\Rightarrow\frac{AC}{BC}=\frac{AH}{AB}\)( các đoạn tương ứng tỉ lệ )
\(\Rightarrow\frac{8}{10}=\frac{AH}{6}\)
\(\Rightarrow AH=4,8\)(cm)
Từ (4) \(\Rightarrow\frac{HB}{AB}=\frac{HA}{AC}\)
\(\Rightarrow\frac{HB}{6}=\frac{4,8}{8}\)
\(\Rightarrow HB=3,6\)(cm)
Từ (5) \(\Rightarrow HC=6,4\left(cm\right)\)

Bạn ơi đề phải là cm góc IHK = 90 độ
Xét tam giác BHA vuông tại H có HI là trung tuyến => HI = 1/2BH = IA => tam giác HIA cân tại I => góc IHA = góc IAH
Tương tự: góc KHA = góc KAH
=> góc IHK = góc IHA + góc KHA = góc IAH + góc KAH = góc BCA = 90 độ
=> ĐPCM

A B C D H E I K O
Gọi Q và O lần lượt là giao điểm cuarDH và AB; HE và AC. ( Điểm Q chưa ký hiệu trên hình vì nhỏ quá nhé ).
Ta dễ dàng chứng minh được: tam giác vuông KHO = tam giác vuông KEO ( hai cạnh góc vuông )
=> \(\widehat{HKO}=\widehat{EKO}\)<=> KO là phân giác ngoài của tam giác IKH ( 1 )
Do \(AH\perp BC\)=> HC là phân giác ngoài của tam giác IKH ( 2 )
Mà KO cắt HC tại C ( 3 ). Từ ( 1 ); ( 2 ) và ( 3 ) => IC là phân giác trong của tam giác IKH <=> \(\widehat{HIC}=\widehat{CIK}=\frac{1}{2}\widehat{HIE}\)( * )
Ta dễ dàng chứng minh được : tam giác vuông DIQ = tam giác vuông HIQ ( hai cạnh góc vuông ) => \(\widehat{DIQ}=\widehat{QIH}=\frac{1}{2}\widehat{DIH}\)( # )
Do D; I ; E thẳng hàng ( theo bài ra ) nên \(\widehat{DIH}+\widehat{HIE}=180^o\)( % )
Từ ( * ); ( # ) và ( % ) => \(\widehat{QIH}+\widehat{HIC}=\frac{1}{2}\widehat{DIH}+\frac{1}{2}\widehat{HIE}\Leftrightarrow\widehat{BIC}=\frac{1}{2}\left(\widehat{DIH}+\widehat{HIE}\right)=\frac{1}{2}.180^o=90^o\)
Do hai góc AIC và BIC là hai góc nằm ở vị trí kề bù nên : \(\widehat{AIC}+\widehat{BIC}=180^o\Leftrightarrow\widehat{AIC}=180^o-\widehat{BIC}=180^o-90^o=90^o\)
Tương tự, ta chứng minh được \(\widehat{AKB}=90^o\)Vậy số đo \(\widehat{AIC},\widehat{AKB}\)đều là \(90^o.\)

a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
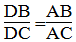
Suy ra:
Suy ra:
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)
b. Ta có: SABC =1/2.AB.AC =1/2.AH.BC
Suy ra: AB.AC = AH.BC
Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90o
Theo định lí Pi-ta-go, ta có: AB2 = AH2 + HB2
Suy ra: HB2 = AB2 - AH2 = 122 - (9,6)2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 607 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠(AHD) = 90o
Theo định lí Pi-ta-go, ta có:
AD2 = AH2 + HD2 = (9,6)2 + (1,37)2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)

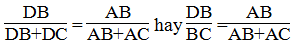
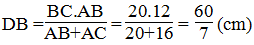
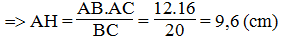
cg ;ơhgyf