Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

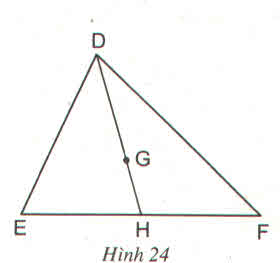
G là trọng tâm của tam giác DEF với đường trung tuyến DH. Khẳng định đúng là:
GHDH=13GHDH=13 vì GHDG=23GHDG=23
nên DH−GHDH=3−23DH−GHDH=3−23
Tức là: GHDH=13GHDH=13

Trong các khẳng định sau:
- Khẳng định c) là đúng.
- Khẳng định a) ; b) là sai.

Chọn (A), (B), (C)
Không chọn (D), vì AG là đường trung tuyến, đã là đường trung tuyến thì không thể nào là đường cao được (đường trung tuyến AG là đường cao khi và chỉ khi tam giác ABC cân ở A).

a) Ta có: f(-1)=1-8.(-1)=1+8=9
Vậy f(-1)=9 là đúng
b) Ta có: f(\(\frac{1}{2}\))=1-8.\(\frac{1}{2}\)=1-4=-3
Vậy f(\(\frac{1}{2}\))=-3 là đúng
c) Ta có: f(3)=1-8.3=1-24=-23
Vậy f(3)=25 là sai

MÌNH GIẢI BÀI 3 NHÉ
GỌI ĐỘ DÀI CÁC CẠNH LẦN LƯỢT LÀ A,B,C (CM) (A,B,C>0)
CÁC CẠNH CỦA TAM GIÁC TỈ LỆ VỚI 3;4;5
A/3=B/4=C/5
CHU VI CỦA TAM GIÁC LÀ 24 CM
A+B+C=24
ÁP DỤNG TÍNH CHẤT CỦA DÃY TỈ SỐ BẰNG NHAU
A/3=B/4=C/5=A+B+C/3+4+5=24/12=2
A/3=2 SUY RA A=6 (TM)
B/4=2 SUY RA B=8 (TM)
C/5=2 SUY RA C=10 (TM)
VẬY; CẠNH 1 ; 6 CM
CẠNH 2; 8 CM
CẠNH 3; 10 CM

Hàm số y = f(x) = 1 – 8x
a) f(-1) = 1 - 8.(-1) = 1 + 8 => Khẳng định f(-1) = 9 đúng
b) f(12)=1−8.12=1−4=−3f(12)=1−8.12=1−4=−3
=> Khẳng định f(12)=−3f(12)=−3 đúng
c) f(3) = 1 - 8. 3 = 1 - 24 = -23 => Khẳng định f(3) = 25 sai
y = f (x) = 1 - 8x
a) f (-1) = 1 - 8.(-1) = 1 - (-8) = 1+8 = 9
Vậy khẳng định f (-1) = 9 là đúng
b) f \(\left(\dfrac{1}{2}\right)\) = 1 - 8. \(\dfrac{1}{2}\) = 1 - 4 = -3
Vậy khẳng định f \(\left(\dfrac{1}{2}\right)\) = -3 là đúng
c) f (3) = 1 - 8 .3 = 1 - 24 = -23
Vậy khẳng định f (3) = 25 là sai

a) Ta có \(\Delta ADC=\Delta ABE\) (c-g-c) => \(\Rightarrow\widehat{ADC}=\widehat{ABE}\)(2 c t/ứ )
Gọi giao điểm của AB và CD là K
Ta có: \(\widehat{ADK}+\widehat{AKD}+\widehat{DAK}=180^0\) (Đl Py-ta-go)
\(\widehat{BMK}+\widehat{BKM}+\widehat{KBM}=180^0\)(Đl Py-ta-go)
\(\Rightarrow\widehat{BMK}=\widehat{KAD}=60^0\)\(\Rightarrow\widehat{BMC}=120^0\)
Gọi J là trung điểm DM
C/m \(\Delta DJB=\Delta AMB\) rồi c/m được \(\widehat{BMA}=120^0\)
rồi suy ra \(\widehat{AMC}=120^0\) \(\Rightarrow\)\(\widehat{AMB}=\widehat{AMC}=\widebat{BMC}\)
Chọn B
A. AG = 3AG ⇒ Vô lý, sai.
B. AG = 2GM ⇒ Đúng (vì AG:GM = 2:1).
C. 3AM = 2AG ⇒ Sai, vì AG = (2/3)AM, nên 3AM = 4.5AG.
D. AM = 1:2GM ⇒ Sai, vì GM = (1/3)AM ⇒ AM = 3GM, không phải 1:2.