Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
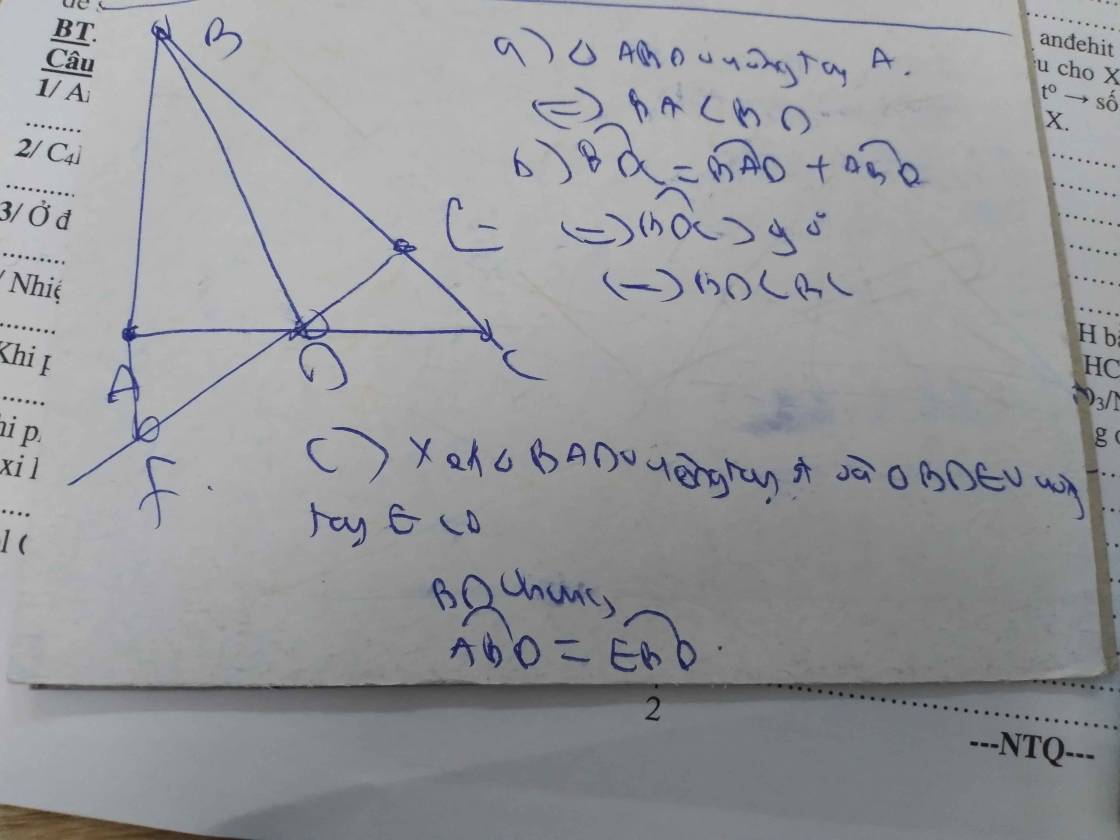
a) Xét ∆ADE và ∆ADB ta có:
AE = AB (gt)
(AD là tia phân giác của )
AD (cạnh chung)
Do đó ∆ADE = ∆ADB (c.g.c)
Mà là góc ngoài của tam giác ADE
Nên
b) Ta có là góc ngoài của tam giác ACD)
Mà (câu a)
∆CDE có DC > ED (định lí cạnh đối diện với góc lớn hơn)
Mà ED = BD (∆ADE = ∆ADB). Do vậy DC>BD.
Câu 1)
A )Ta có tam giác ABC cân tại A
=> \(\widehat{ABC}=\widehat{ACB}\)
Và AB = AC
Xét hai tam giác vuông BCK và CBH ta có :
BC chung
\(\widehat{KBC}=\widehat{BCH}\)
=>BCK = CBH (cạnh huyền - góc nhọn )
=>BH = CK (đpcm)
B) ta có BCK = CBH
=> \(\widehat{HBC}=\widehat{KCB}\)
=> \(\widehat{ABH}=\widehat{ACK}\)
=> tam giác OBC cân tại O
=> BO = CO
Xét tam giác ABO và tam giác ACO
AB = AC
BO = CO (cmt)
\(\widehat{ABH}=\widehat{ACK}\)
=> ABO=ACO (c-g-c)
=> \(\widehat{BAO}=\widehat{CAO}\)
=> AO là phân giác góc ABC (đpcm)
C) ta có
AI là phân giác góc ABC
Mà tam giác ABC cân tại A
=> AI vuông góc với cạnh BC (đpcm)
Bài 1:
Xét ΔABC có AD là phân giác
nên BD/AB=CD/AC
mà AB>AC
nên BD>CD
