CC
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
H9
HT.Phong (9A5)
CTVHS
23 tháng 3 2023
Do \(BM\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AM=CM\)
Và \(CN\) là đường trung tuyến của \(\Delta ABC\) nên ta có: \(AN=BN\)
Mà \(BM=CN\left(gt\right)\)
Từ đó suy ra: \(AM=CM=AN=BN\)
Ta lại có: \(AM+CM=AC\)
Và \(AN+BN=AB\)
Nên: \(AM=CM=AN=BN\)
\(\Rightarrow AM+CM=AN+BN\)
\(\Rightarrow AC=AB\)
Vậy \(\Delta ABC\) có \(AC=AB\) là tam giác cân tại \(A\)
NN
2
H9
HT.Phong (9A5)
CTVHS
28 tháng 3 2023
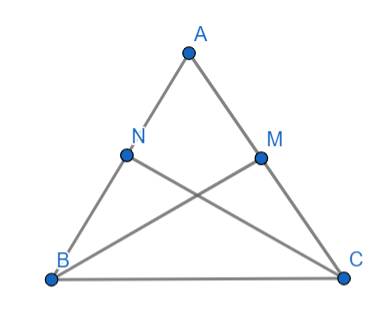
Xét △AMB và △ANC ta có:
AM=AN ( Vì M,N lần lượt là trung điểm của 2 cạnh AB, AC)
\(\widehat{A}\) là góc chung
AB=AC (Vì là hai cạnh bên trong tam giác cân)
\(\Rightarrow\Delta AMB=\Delta ANC\left(c-g-c\right)\)
\(\Rightarrow BM=CN\) (hai cạnh tương ứng)
27 tháng 3 2023
Xét ΔAMB và ΔANC có
AM=AN
góc A chug
AB=AC
=>ΔAMB=ΔANC
=>BM=CN
21 tháng 9 2023
Tham khảo:
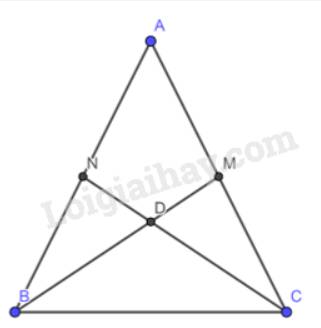
Gọi D là giao điểm của CN và BM
\( \Rightarrow \) D là trọng tâm tam giác ABC
\( \Rightarrow CD = \dfrac{2}{3}CN = BD = \dfrac{2}{3}BM\) ( do BM = CN )
\( \Rightarrow \) tam giác DBC cân tại D do BD = CD
\( \Rightarrow \) \(\widehat {DBC} = \widehat {DCB}\)(2 góc đáy trong tam giác cân) (1)
Xét \(\Delta NDB\) và \(\Delta MDC\) có :
BD = CD
\(\widehat {NDB} = \widehat {MDC}\) (2 góc đối đỉnh)
ND = DM (do cùng \( = \dfrac{1}{3}CN = \dfrac{1}{3}BM\) (tính chất của trung trực đi qua trọng tâm tam giác ))
\( \Rightarrow \Delta NDB=\Delta MDC\) (c.g.c)
\( \Rightarrow \,\widehat {NBD} = \widehat {MCD}\)(2 góc tương ứng) (2)
Từ (1) và (2) \( \Rightarrow \widehat {ABC} = \widehat {ACB}\) do \(\widehat {ABC} = \widehat {NBD} + \widehat {DBC}\) và \(\widehat {ACB} = \widehat {MCD} + \widehat {DCB}\)
\( \Rightarrow \Delta ABC\) cân tại A (do 2 góc bằng nhau)
BN
0
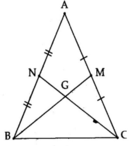
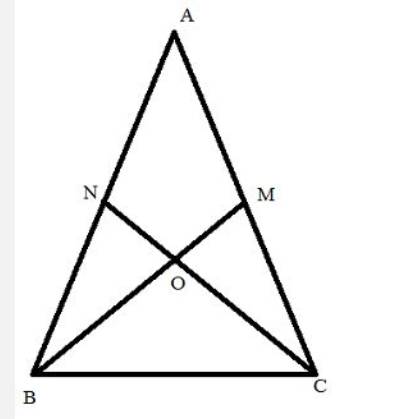
tu ve hinh :
xet tamgiac BCN va tamgiac CBM co : BC chung
BM = CN (gt)
goc BMC = goc CNB = 90 do BM va CN la duong cao (gt)
=> tamgiac BCN = tamgiac CBM (ch - cgv)
=> goc ABC = goc ACB (dn)
=> tamigac ABC can tai A (gt)
dong cuoi ghi lon, k phai gt ma la dn :v