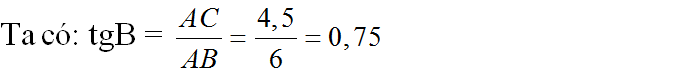Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mình chỉ biết bài 3 thôi. hai bài kia cx làm được nhưng ngại trình bày
A B C 4 9
Ta có : BC = BH +HC = 4 + 9 = 13 (cm)
Theo hệ thức lượng trong tam giác vuông ta có:
- AC2 = BC * HC
AC2 = 13 * 9 = 117
AC = \(3\sqrt{13}\)(cm)
- AB2 =BH * BC
AB2 = 13 * 4 = 52
AB = \(2\sqrt{13}\)(CM)

a, bạn dễ dàng chứng minh được tam giác ABC vuông tại A theo định lí Py-ta-go đảo
-áp dụng tỉ số lượng giác sinB = \(\frac{4,5}{7,5}\)=> góc B= 37o => góc C = 53o
-áp dụng HTL cho tam giác vuông ABC có đường cao AH: AH.BC = AB.AC => AH = 3,6 (cm)

A B C 30o 9 H 18 D
a, ^B = ^A - ^C = 900 - 300 = 600
\(\cos B=\frac{AB}{AC}\Rightarrow\frac{1}{2}=\frac{9}{AC}\Rightarrow AC=18\)cm
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2=81+324=405\Rightarrow BC=9\sqrt{5}\)cm
b, \(\cos B=\frac{BH}{AB}\Rightarrow\frac{1}{2}=\frac{BH}{9}\Rightarrow BH=\frac{9}{2}\)cm
\(\sin B=\frac{AH}{AB}\Rightarrow\frac{\sqrt{3}}{2}=\frac{AH}{9}\Rightarrow AH=\frac{9\sqrt{3}}{2}\)cm
c, Vì AD là đường phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow\frac{DC}{AC}=\frac{BD}{AB}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{DC}{AC}=\frac{BD}{AB}=\frac{DC+BD}{AC+AB}=\frac{9\sqrt{5}}{27}=\frac{\sqrt{5}}{3}\)
\(\Rightarrow BD=\frac{\sqrt{5}}{3}AB=\frac{\sqrt{5}}{3}.9=3\sqrt{5}\)cm
\(\Rightarrow HD=BD-BH=3\sqrt{5}-\frac{9}{2}\)cm
Áp dụng định lí tam giác AHD vuông tại H ta có :
\(AD^2=AH^2+HD^2=\left(\frac{9\sqrt{3}}{2}\right)^2+\left(3\sqrt{5}-\frac{9}{2}\right)^2\)
tự giải nhé ><
a. Giải tam giác ABC
B=60^0
AC=AB/tan30=9.√ 3
BC=AB/sin30=9.2 =18
S=AC.AB/2=81√ 3/2
b. Kẻ AH là đường cao, tính AH, BH
AH=2S/BC=81√ 3/18=9√ 3/2
BH=√ (AB^2-AH^2)=9√ (1-3/4)=9/2

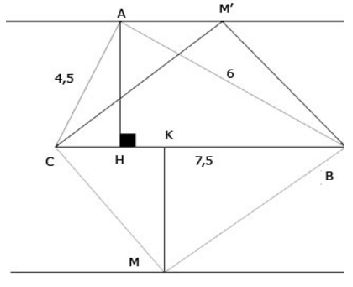
b)Để SMBC = SABC thì M phải cách BC một khoảng bằng AH. Do đó M phải nằm bên trên hai đường thẳng song song với BC, cách BC một khoảng bằng 3,6cm.

a)ta thấy AB^2+AC^2=56.25 và BC^2=56.25
=>AB^2+BC^2=BC^2<=>tam jác ABC vuông tại A
Sin B=AC/BC=4.5/7.5<=>B=36độ 52 phút 11.63 giây (bấm shift sin 4.5/7.5 =)
sin c=AB/BC =>C=53đô 7 phút 48.37 giây
Sin C=AH/Ac =>AH=sin C*AC=3.6
b)qua A kẻ đường thẳng d song song BC.diện tích tam jác ABC luôn bằng diện tích tam jác BMC khi M thuộc d.(vì MH sẽ luôn = AH