Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

có 3 cách
cách 1

cách 2

cách 3
a) vì A trung điểm DH
E trung điểm HC
=>F là trọng tâm tam giác DHC
=>HF cắt CD tại TĐ K của CD
b) vì F là trọng tâm tam giác HDC nên HF/HK=1/3
mà HK=1/2CD (do tam giác DHC vuông có HK là trung tuyến)
=>HF=1/3 CD

k nha

Xét ΔBAD có
BH là đường cao
BH là đường trung tuyến
Do đó: ΔBAD cân tại B
Ta có: ΔBAD cân tại B
mà BH là đường cao
nên BH là tia phân giác của góc ABD


a) \(BEH\)cân tại \(B\)nên \(\widehat{E}=\widehat{H_1}\)
\(\widehat{ABC}=\widehat{E}+\widehat{H_1}=2\widehat{E}\)
\(\widehat{ABC}=2\widehat{C}\)
\(\Rightarrow\widehat{BEH}=\widehat{ACB}\)
b) Chứng minh được \(\Delta DHC\)cân tại \(D\)nên \(DC=DH\)
\(\Delta DHC\)có :
\(\widehat{DAH}=90^0-\widehat{C}\)
\(\widehat{DHA}=90^0-\widehat{H}_2=90^0-\widehat{C}\)
\(\Rightarrow\Delta DAH\)cân tại \(D\)nên \(DA=DH\)
c) \(\Delta ABB'\)cân tại \(A\)nên :
\(\widehat{B'}=\widehat{B}=2\widehat{C}\)
\(\widehat{B'}=\widehat{A_1}+\widehat{C}\)
\(\Rightarrow2\widehat{C}=\widehat{A_1}+\widehat{C}\)
\(\Rightarrow\widehat{C}=\widehat{A_1}\)
\(\Rightarrow\widehat{AB'C}\)cân tại \(B'\)
d) \(AB=AB'=CB'\)
\(BE=BH=B'H\)
Có : \(AE=AB+BE\)
\(HC=CB'+B'H\)
\(\Rightarrow AE=HC\)

a: Xét ΔAHB vuông tại H và ΔDHB vuông tại H có
BH chung
HA=HD
Do đó: ΔAHB=ΔDHB
b: Ta co: ΔAHB=ΔDHB
nên góc ABH=góc DBH
=>BH là phân giác của góc ABD
Ta có: ΔBAD cân tại B
mà BC là đường cao
nên BC là trung trực của AD
c: Xét ΔABC và ΔDBC có
BA=BD
góc ABC=góc DBC
BC chung
Do đó: ΔABC=ΔDBC

a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
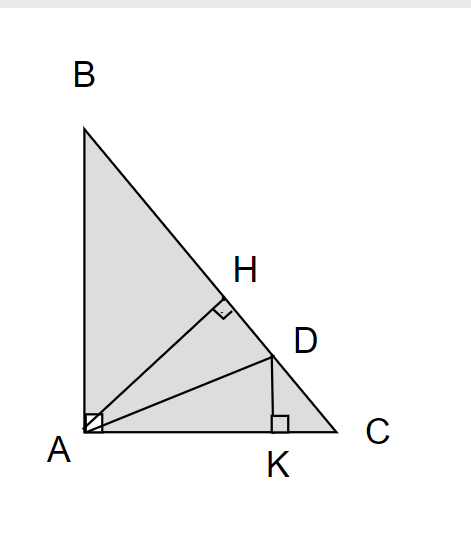
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)
hình tự vẽ nha bn
tam giac ADC có CH là đường cao đồng thời là trung tuyến ( H là tđ của AD, đường cao AH)
=> tam giac ADC cân tại C
tam giac ADC cân tại C có CH là đường cao => CH là pg=>góc C1=C2
XÉT tam giac ABC và tam giac DBC có
AC=DC,GÓC C1=C2,BC CẠNH CHUNG
=> tam giac ABC=tam giac DBC (C-G-C)
=> GÓC ABC=GÓC DBC