Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔACD có \(\hat{ACB}\) là góc ngoài tại đỉnh C
nên \(\hat{ACB}=\hat{CAD}+\hat{CDA}=2\cdot\hat{CDA}\)
Xét ΔDAB có \(\hat{xAB}\) là góc ngoài tại đỉnh A
=>\(\hat{xAB}=\hat{ABD}+\hat{ADB}=2\cdot\hat{CDA}+\hat{CDA}=3\cdot\hat{CDA}\)
b: ΔABC cân tại A
=>\(\hat{BAC}=180^0-2\cdot\hat{ABC}=180^0-2\cdot50^0=80^0\)
\(\hat{ABC}=2\cdot\hat{CDA}\)
=>\(\hat{CDA}=\frac{50^0}{2}=25^0\)
Ta có: \(\hat{CDA}=\hat{CAD}\)
mà \(\hat{CDA}=25^0\)
nên \(\hat{CAD}=25^0\)
c: CM là phân giác của góc ACB
=>\(\hat{ACM}=\frac12\cdot\hat{ACB}\) (1)
Ta có: ΔCAD cân tại C
=>\(\hat{CAD}=\hat{CDA}\)
=>\(\hat{CAD}=\frac12\cdot\hat{ACB}\) (2)
Từ (1),(2) suy ra \(\hat{ACM}=\hat{CAD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AD//CM
Ta có: AD//CM
AD⊥ Ay
Do đó: Ay⊥CM

a: Ta có: \(\widehat{ABC}+\widehat{DBC}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{BCE}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)
nên \(\widehat{DBC}=\widehat{BCE}\)
Xét ΔDBC và ΔECB có
BD=CE
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
=>DC=EB
ΔDBC=ΔECB
=>\(\widehat{BCD}=\widehat{CBE}\)
=>\(\widehat{IBC}=\widehat{ICB}\)
=>ΔIBC cân tại I
=>IB=IC
Ta có: IB+IE=BE
IC+ID=CD
mà IB=IC và BE=CD
nên IE=ID
b: Xét ΔABC có \(\dfrac{AB}{BD}=\dfrac{AC}{CE}\)
nên BC//DE
c: Ta có: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: MB=MC
=>M nằm trên đường trung trực của BC(2)
Ta có: IB=IC
=>I nằm trên đường trung trực của BC(3)
Từ (1),(2),(3) suy ra A,M,I thẳng hàng

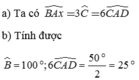
rac roi roi day.Sorry bn nha