Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Vì BD là phân giác của \(\widehat{ABC}\) nên \(\widehat{ABD}=\widehat{DBC}=\frac{1}{2}\widehat{ABC}\)
Lại có \(\widehat{EBD}=\widehat{EDB}\)(gt)
=> \(\widehat{EDB}=\widehat{DBC}\)
Mà 2 góc ở vị trí so le trong nên ED//BC
Chúc bạn làm bài tốt!!!!
b) Vì ED//BC nên \(\widehat{AED}=\widehat{ABC}\)(đồng vị) (1)
Vì EF//BD nên \(\widehat{AEF}=\widehat{ABD}\)(đồng vị) (2)
Lại có \(\widehat{ABD}=\frac{1}{2}\widehat{ABC}\)(cmt) (3)
Từ (1),(2) và (3) suy ra \(\widehat{AEF}=\frac{1}{2}\widehat{AED}\)
=> EF là tia phân giác của góc AED
Chúc bạn làm bài tốt !!!!!!!!!!

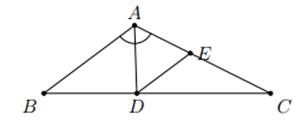
\(\text{Đặt AD=DE=EA=x. Ta có}\)
\(\text{Đặt AD=DE=EA=x. Ta có:}\)
\(\dfrac{DE}{AB}=\dfrac{CE}{CA}=\dfrac{x}{3}=\dfrac{6-x}{6}\)
\(\Rightarrow x=2\). \(\text{Vậy}\) \(AD=2cm\)

a) DM = ME, DK = KC => MK // EC hay MK//AC
b) MK//AC, KN//BD => ^KNM = ^A = 80 độ
KN = 1/2BD, MK = 1/2 EC, mà BD = EC => KN = MK => MNK là t/g cân
=> ^MNK = ^NMK = (180-80)/2 = 50 độ

a: \(\widehat{FDE}=360^0-120^0-90^0-90^0=60^0\)
Xét ΔAED vuông tại E và ΔAFD vuông tại F có
AD chung
\(\widehat{EAD}=\widehat{FAD}\)
Do đó: ΔAED=ΔAFD
Suy ra: DE=DF và AE=AF
Xét ΔDEF có DE=DF
nên ΔDEF cân tại D
mà \(\widehat{FDE}=60^0\)
nên ΔDEF đều
b: Xét ΔADK và ΔADI có
AK=AI
\(\widehat{KAD}=\widehat{IAD}\)
AD chung
Do đó:ΔADK=ΔADI
Suy ra: DK=DI
hay ΔDKI cân tại D

giup mk làm câu c vs