Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b: Xét tứ giác AFBC có
E là trung điểm của AB
E là trung điểm của CF
Do đó: AFBC là hình bình hành
Suy ra: AC//BF

a) Xét △ACE và △BFE có:
EA=EB(E là trung điểm của AB) gócAEC=gócFEB(2 góc đối đỉnh)EC=EF(gt)
⇒△ACE = △BFE(c.g.c)(đpcm)
b) Có: △ACE = △BFE (cmt)
⇒gócACE=gócBFE(2 góc tương ứng)
Mà 2 góc ở vị trí so le trong
⇒ AC // BF (dấu hiệu nhận biết)
c) Có AC // BF (cmt)
⇒gócEBA=gócBAC(2 góc so le trong)
Xét △ACB và △BFA có:
+AC=BF(cmt) +gócEBA=gócBAC(cmt) +ABlà cạnh chung
⇒△ACB = △BFA(c.g.c)(đpcm)

a: Xét ΔAEC và ΔBEF có
EA=EB
\(\widehat{AEC}=\widehat{BEF}\)
EC=EF
Do đó: ΔAEC=ΔBEF
b) Ta có: △ AEC và △ BEF ( chứng minh trên )
Mà lại có: \(\widehat{ACE}=\widehat{BFE}\) ( 2 góc tương ứng )
Ta lại thấy hai góc này ở vị trí so le trong
Suy ra: AC // BF

1, Xét tam giác ABC có : A+B+C=180
=> ACB=180-A-B=40độ
2, Vì DE//BC nên ta có : góc ADE=DBF ( đồng vị )
Xét tam giác ADE và DBF có :
AD=DB
DE=BF
góc ADE=DBF
=> tam giác ADE=DBF (c.g.c)
b, vì tam giác ADE=DBF nên góc BDF=DAE ( hai góc đồng vị bằng nhau ) => DF//AC.
c, Xét tam giác ABC có : AD=BD và DF//AC => BF=FC
1) A + B + C = 180 độ
C = 180 độ - ( 60 độ + 80 độ )
C = 40 độ
2)
a) Xét t/giác EDA và FBD , có
Có góc EDA = góc FBD ( 2 đường ED // CB)
AD = DB ( D là trung điểm của AB )
FB = ED ( gt )
=> t/giác EDA = t/giác FBD ( c.g.c )
b) Ta có: góc A = góc FDB ( t/giác EDA = t/giác FBD)
mà chúng ở vị trí so le trong => FD // EA hay FD // CA
c) bí

a) Xét ΔADB và ΔAEC có:
AB=AC(gt)
A: chung
AD=AE(gt)
=>ΔADB=ΔAEC(c.g.c)
=>đpcm
b) Có: AB=AC
=>ΔABC cân ở A
=>ABC=ACB(t/c Δ cân)
=>ABD+DBC=ACE+ECB
Mà ABD=ACE(ΔADB=ΔAEC)
=>DBC=ECB
=>ΔBCF cân ở F
=>BF=CF(t/c Δ cân)
c) Ta có:
AB=AE+EB
AC=AD+DC
Mà AB=AC; AE=AD
=>EB=DC
Xét ΔEBC và ΔDCB có:
EB=DC(cmt)
EBC=DCB(ΔABC cân)
BC: chung
=>ΔEBC=ΔDCB(c.g.c)
=>CEB=BDC(hai cạnh tương ứng)
Mà AEC+BEC=ADB+CDB=180°
=>AEC=ADB
Ta có:
EC=EF+FC
BD=BF+FD
Mà EC=BD(ΔEBC=ΔDCB); BF=CF(cmt)
=>FE=FD
Xét ΔAFE và ΔAFD có:
AE=AD(gt)
AEF=ADF(cmt)
FE=FD(cmt)
=>ΔAFE=ΔAFD(c.g.c)
=>EAF=DAF(hai góc tương ứng)
=>AF là pg BAC(1)
Xét ΔHAB và ΔHAC có:
ABH=ACHF(ΔABC cân)
HB=HC(H là trđ BC)
BAH=CAH(cmt)
=>ΔHAB=ΔHAC(g.c.g)
=>BAH=CAH(hai góc tương ứng)
=>AH là pg BAC(2)
Từ (1) và (2)
=>A, F, H thuộc thẳng hàng
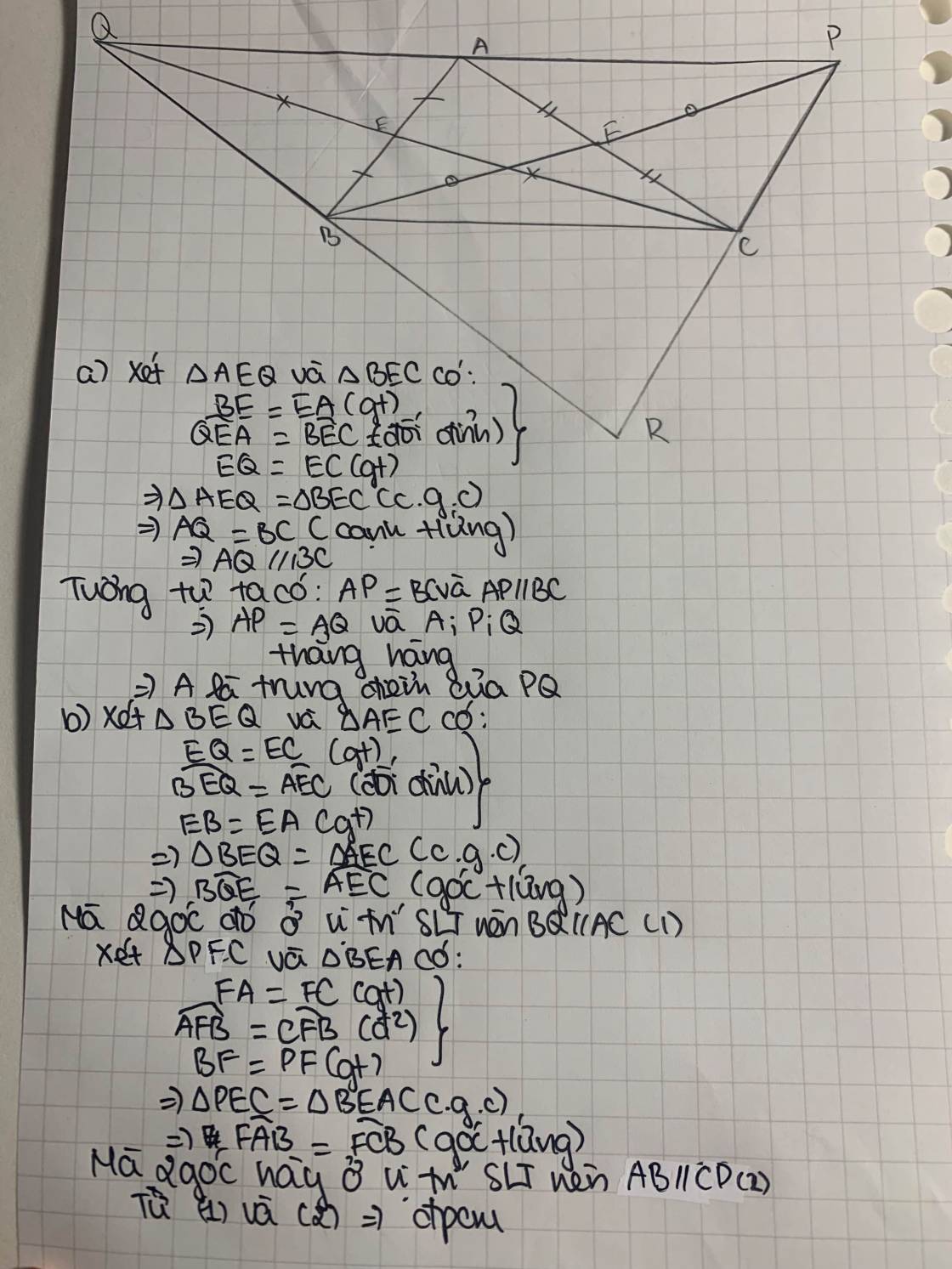
a) Xét △ACE và △BFE có:
\(\left\{{}\begin{matrix}EA=EB\left(\text{E là trung điểm của AB}\right)\\\widehat{AEC}=\widehat{FEB}\left(\text{2 góc đối đỉnh}\right)\\EC=EF\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\text{△ACE = △BFE}\left(c.g.c\right)\)
\(\Rightarrow AC=BF\left(\text{2 cạnh tương ứng}\right)\)
b) Có: △ACE = △BFE (cmt)
\(\Rightarrow\widehat{ACE}=\widehat{BFE}\left(\text{2 góc tương ứng}\right)\)
Mà 2 góc ở vị trí so le trong
\(\Rightarrow\) AC // BF (dấu hiệu nhận biết)
c) Có AC // BF (cmt)
\(\Rightarrow\widehat{EBA}=\widehat{BAC}\left(\text{2 góc so le trong}\right)\)
Xét △ACB và △BFA có:
\(\left\{{}\begin{matrix}AC=BF\left(cmt\right)\\\widehat{EBA}=\widehat{BAC}\left(cmt\right)\\AB:\text{cạnh chung}\end{matrix}\right.\)
\(\Rightarrow\text{△ACB = △BFA}\left(c.g.c\right)\)
Hình bạn tự vẽ nha!
a) Xét 2 \(\Delta\) \(ACE\) và \(BFE\) có:
\(AE=BE\) (vì E là trung điểm của \(AB\))
\(\widehat{AEC}=\widehat{BEF}\) (vì 2 góc đối đỉnh)
\(CE=FE\) (vì E là trung điểm của \(CF\))
=> \(\Delta ACE=\Delta BFE\left(c-g-c\right)\)
=> \(AC=BF\) (2 cạnh tương ứng).
b) Theo câu a) ta có \(\Delta ACE=\Delta BFE.\)
=> \(\widehat{ACE}=\widehat{BFE}\) (2 góc tương ứng).
Mà 2 góc này nằm ở vị trí so le trong.
=> \(AC\) // \(BF.\)
Vì \(AC\) // \(BF\left(cmt\right).\)
=> \(\widehat{CAB}=\widehat{FBA}\) (vì 2 góc so le trong).
c) Xét 2 \(\Delta\) \(ACB\) và \(BFA\) có:
\(AC=BF\left(cmt\right)\)
\(\widehat{CAB}=\widehat{FBA}\left(cmt\right)\)
Cạnh AB chung
=> \(\Delta ABC=\Delta BFA\left(c-g-c\right)\left(đpcm\right).\)
Chúc bạn học tốt!